Przedstawione na rysunku trójkąty są podobne.
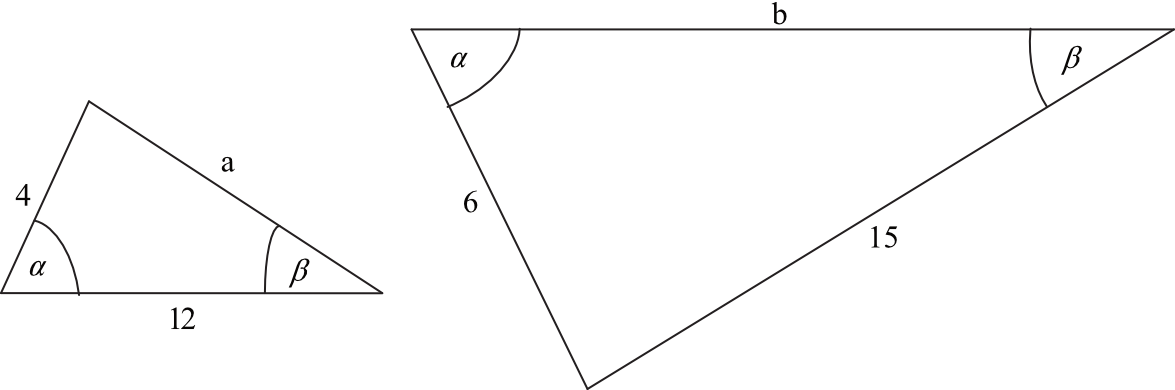
Wówczas:
\(a=13,\;b=17\)
\(a=10,\;b=18\)
\(a=9,\;b=19\)
\(a=11,\;b=13\)
Rozwiązanie:
Podobieństwo trójkątów oznacza, że stosunek długości poszczególnych boków jest taki sam w obydwu figurach. To z kolei pozwoli nam ułożyć równania, dzięki którym wyznaczymy długości boków \(a\) oraz \(b\). Musimy tylko uważać, aby dobrze zapisać odniesienia do poszczególnych boków.
Krok 1. Wyznaczenie długości boku \(a\).
$$\frac{4}{6}=\frac{a}{15} \quad\bigg/\cdot30 \\
20=2a \\
a=10$$
Krok 2. Wyznaczenie długości boku \(b\).
$$\frac{4}{6}=\frac{12}{b}$$
Mnożąc na krzyż otrzymamy:
$$4b=72 \\
b=18$$
Odpowiedź:
B. \(a=10,\;b=18\)

