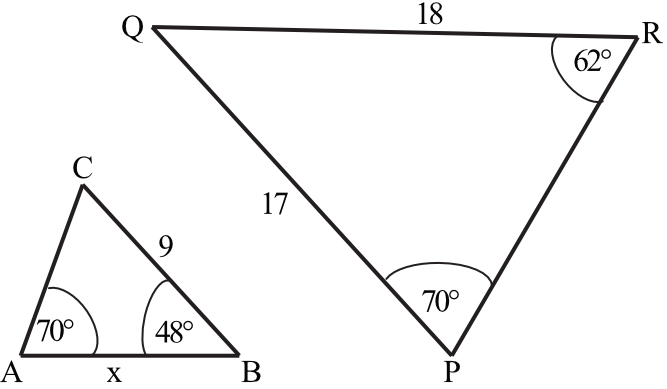
Przedstawione na rysunku trójkąty \(ABC\) i \(PQR\) są podobne. Bok \(AB\) trójkąta \(ABC\) ma długość:
\(8\)
\(8,5\)
\(9,5\)
\(10\)
Rozwiązanie:
Aby zrozumieć istotę zadania musimy sobie powiedzieć skąd wiemy, że te dwa trójkąty są podobne. Wynika to z cechy kąt-kąt-kąt, bo:
$$|\sphericalangle ACB|=180°-70°-48°=62° \\
\text{oraz} \\
|\sphericalangle PQR|=180°-70°-62°=48°$$
Skoro trójkąty \(ABC\) i \(PQR\) są podobne, to znaczy że stosunki długości poszczególnych boków (leżących przy tych samych kątach) będą jednakowe. Zatem:
$$\frac{|AB|}{|BC|}=\frac{|PQ|}{|QR|} \\
\frac{x}{9}=\frac{17}{18}$$
Takie równanie najprościej jest rozwiązać mnożąc na krzyż:
$$18x=17\cdot9 \\
18x=153 \\
x=8,5$$
Odpowiedź:
B. \(8,5\)

