Przygotowałem dla Was pewniaki maturalne, czyli 38 klasycznych typów zadań, które zazwyczaj pojawiają się na maturze z matematyki na poziomie podstawowym. Do każdego typu zadania dopasowałem dwa charakterystyczne zadania z danego zagadnienia. Można więc powiedzieć, że jest to szybki przegląd zadań maturalnych, idealny na powtórkę przed egzaminem. To co jest najważniejsze, to wszystkie zadania pochodzą z matur, są to więc realne przykłady, które już kiedyś na maturze wystąpiły.
Ale to nie wszystko. Aby pewniaki były dla Was jak najbardziej wartościowe, to do każdego zagadnienia napisałem dwie podpowiedzi. Pierwsza podpowiedź jest merytoryczna i jej zadaniem jest przypomnienie Wam jakiejś najistotniejszej lub najbardziej problematycznej rzeczy w danym temacie. Druga podpowiedź jest taką ostatnią deską ratunku, która ma na celu doprowadzić Was do poprawnej odpowiedzi albo przynajmniej wykluczenia jakiegoś wariantu (co sprawi, że mamy większe szanse na dobre strzelenie).
Jeżeli potrzebujecie dokładnego omówienia jakiegoś zagadnienia maturalnego, to polecam filmiki które znajdziecie w moim kursie: Kurs maturalny
Pewniaki maturalne
1. Działania na potęgach
Podpowiedź: W takich zadaniach zazwyczaj trzeba sprowadzić liczby do wspólnej podstawy potęgi (lub wspólnego wykładnika), bo wtedy możemy wykonywać kluczowe działania na potęgach.
Ostatnia deska ratunku: W awaryjnych sytuacjach można próbować wyliczyć poszczególne wartości na kalkulatorze i sprawdzić w ten sposób przynajmniej przybliżoną wartość danego działania. Wbrew pozorom większość zadań da się w ten sposób rozwiązać.
- Rozwiązanie:
Musimy wykonać działania na potęgach, pamiętając że \(32=2^5\) oraz \(\frac{1}{8}=2^{-3}\), zatem:
$$32^{-3}:\left(\frac{1}{8}\right)^4=(2^5)^{-3}:(2^{-3})^4= \\
=2^{5\cdot(-3)}:2^{-3\cdot4}=2^{-15}:2^{-12}=2^{-15-(-12)}=2^{-3}$$ - Odpowiedź:
B. \(2^{-3}\)
- Rozwiązanie:
Liczbę \(45\) znajdującą się w mianowniku możemy rozbić na iloczyn \(9\cdot5\), zatem:
$$\require{cancel}
\frac{9^5\cdot5^9}{45^5}=\frac{9^5\cdot5^9}{(9\cdot5)^5}=\frac{\cancel{9^5}\cdot5^9}{\cancel{9^5}\cdot5^5}= \\
=5^9:5^5=5^{9-5}=5^4$$ - Odpowiedź:
D. \(5^{4}\)
2. Działania na pierwiastkach
Podpowiedź: Pierwiastki możemy sprowadzać do postaci potęg np. \(\sqrt{5}=5^{\frac{1}{2}}\), \(\sqrt[3]{5}=5^{\frac{1}{3}}\), \(\sqrt[3]{25}=\sqrt[3]{5^2}=5^{\frac{2}{3}}\) i często będzie to klucz do rozwiązania jakiegoś rozbudowanego ułamka z potęgami i pierwiastkami. Drugą często wykorzystywaną umiejętnością jest wyłączanie czynnika przed znak pierwiastka np. \(\sqrt{48}=\sqrt{16\cdot3}=4\sqrt{3}\).
Ostatnia deska ratunku: Na kalkulatorach mamy jedynie pierwiastki drugiego stopnia. Jak więc policzyć pierwiastki nieco wyższych stopni? Jak naciśniemy na kalkulatorze dwukrotnie przycisk pierwiastka to obliczymy pierwiastek czwartego stopnia, a jak naciśniemy trzykrotnie to obliczymy pierwiastek ósmego stopnia. Tym samym (tak w dużym przybliżeniu) jak mamy gdzieś w zadaniu np. pierwiastek szóstego stopnia, to spodziewamy się, że będzie to wartość mniej więcej między pierwiastkiem czwartego i ósmego stopnia. Taki trik może czasem pozwolić obliczyć jakiś przybliżony wynik i w ten sposób trafimy w poprawną odpowiedź.
- Rozwiązanie:
Musimy rozbić liczbę \(54\) na takie dwa czynniki, aby z jednego z nich dało się wyciągnąć pierwiastek trzeciego stopnia. Zatem:
$$\sqrt[3]{54}-\sqrt[3]{2}=\sqrt[3]{27\cdot2}-\sqrt[3]{2}=3\sqrt[3]{2}-\sqrt[3]{2}=2\sqrt[3]{2}$$ - Odpowiedź:
C. \(2\sqrt[3]{2}\)
- Rozwiązanie:
Wykonując poprawnie działania na pierwiastkach i ułamkach oraz pamiętając, że \(16=4^2\), otrzymamy:
$$(\sqrt[3]{16}\cdot4^{-2})^3=(16^{\frac{1}{3}}\cdot4^{-2})^3= \\
=(16^{\frac{1}{3}})^3\cdot(4^{-2})^3=16^{\frac{1}{3}\cdot3}\cdot4^{-2\cdot3}= \\
=16^1\cdot4^{-6}=4^2\cdot4^{-6}= \\
=4^{2-6}=4^{-4}$$ - Odpowiedź:
B. \(4^{-4}\)
3.Usuwanie niewymierności z mianownika
Podpowiedź: Jak w mianowniku ułamka jest samotny pierwiastek typu \(\sqrt{3}\) to sprawa jest prosta – trzeba wymnożyć licznik i mianownik ułamka właśnie przez \(\sqrt{3}\). Możemy też rozbić liczbę znajdującą się w liczniku na taką, by skróciła nam się z tym pierwiastkiem. Nieco trudniej jest kiedy w mianowniku ułamka mamy wyrażenie typu \(\sqrt{3}-1\), wtedy trzeba wymnożyć licznik i mianownik takiego ułamka przez \(\sqrt{3}+1\), korzystając przy okazji ze wzorów skróconego mnożenia.
Ostatnia deska ratunku: Jeżeli jest to zadanie zamknięte to bardzo często jesteśmy w stanie obliczyć interesującą nas wartość na kalkulatorze, przyrównując otrzymane zaokrąglenie do proponowanych odpowiedzi.
- Rozwiązanie:
To zadanie można rozwiązać na kilka sposobów, ale najprościej będzie chyba rozbić liczbę \(25\) na \(5\cdot\sqrt{5}\cdot\sqrt{5}\), bo wtedy skróci nam się od razu pierwiastek z mianownika. Można też potraktować \(25\) jako \(5^2\), a następnie standardowo usunąć niewymierność z mianownika. Obydwie metody prowadzą skutecznie do tego samego wyniku:
$$\require{cancel}
\frac{5^3\cdot25}{\sqrt{5}}=\frac{5^3\cdot5\cdot\sqrt{5}\cdot\cancel{\sqrt{5}}}{\cancel{\sqrt{5}}}=5^4\sqrt{5}$$ - Odpowiedź:
B. \(5^4\sqrt{5}\)
- Rozwiązanie:
Nie możemy ot tak skrócić sobie licznika z mianownikiem, bo między liczbami stoją znaki dodawania/odejmowania. Musimy tak naprawdę wymnożyć licznik i mianownik przez wartość \(\sqrt{5}+2\), pobywając się w ten sposób niewymierności w mianowniku. Zatem:
$$\frac{\sqrt{5}+2}{\sqrt{5}-2}=\frac{(\sqrt{5}+2)\cdot(\sqrt{5}+2)}{(\sqrt{5}-2)\cdot(\sqrt{5}+2)}= \\
=\frac{5+4\sqrt{5}+4}{5-4}=9+4\sqrt{5}$$ - Odpowiedź:
D. \(9+4\sqrt{5}\)
4. Działania na logarytmach
Podpowiedź: Pamiętaj o tym, że logarytmy można zamieniać na postać potęg: \(log_{a}c=b\), wtedy gdy \(a^b=c\) (tę zależność znajdziesz w tablicach maturalnych).
Ostatnia deska ratunku: Gdy w podstawie logarytmu jest liczba naturalna, a liczbą logarytmowaną jest ułamek, to wynik logarytmu związany jest z liczbą ujemną.
- Rozwiązanie:
Musimy sobie odpowiedzieć na pytanie – do jakiej liczby trzeba podnieść liczbę \(3\), aby otrzymać \(\frac{1}{27}\). Jeśli dobrze orientujemy się w działaniach na potęgach to dobrze wiemy, że skoro wynik jest w formie ułamka to na pewno będzie to liczba ujemna, a dokładnie tą liczbą będzie \(-3\), bo:
$$3^{-3}=\frac{1}{3^3}=\frac{1}{27}$$ - Odpowiedź:
A. \(-3\)
- Rozwiązanie:
Skorzystamy ze wzoru na sumę logarytmów o tej samej podstawie \(\log_{a}x+\log_{a}y=\log_{a}(x\cdot y)\), stąd też:
$$\log_{4}8+\log_{4}2=\log_{4}(8\cdot2)=\log_{4}16=2$$ - Odpowiedź:
B. \(2\)
5. Obliczenia procentowe
Podpowiedź: Pamiętaj, że liczba większa o np. \(20\%\) od liczby \(x\) to \(1,2x\), a liczba o \(20\%\) mniejsza od \(x\) to \(0,8x\).
Ostatnia deska ratunku: Często możemy sprawdzać po kolei liczby z odpowiedzi ABCD i w ten sposób zweryfikujemy która liczba była tą poszukiwaną liczbą którą poddaliśmy jakimś działaniom na procentach.
- Rozwiązanie:
\(15\%\) możemy zapisać w formie ułamka dziesiętnego jako \(0,15\). W związku z tym \(15\%\) z \(x\) jest równe \(0,15\cdot x\). Wiemy, że suma \(x\) oraz \(0,15\cdot x\) jest równa \(230\), zatem poszukiwanym równaniem jest:
$$x+0,15\cdot x=230$$ - Odpowiedź:
C. \(x+0,15\cdot x=230\)
- Rozwiązanie:
\(x\) – tyle oszczędności miała Julia
\(0,5x\) – tyle oszczędności przeznaczyła Julia na prezent dla Maćka
\(x-0,5x=0,5x\) – tyle pieniędzy pozostało Julii po zakupie prezentu
\(0,1\cdot0,5x=0,05x\) – tyle pieniędzy przeznaczyła Julia na prezent dla Dominiki
\(0,5x-0,05x=0,45x\) – tyle pieniędzy pozostało Julii po zakupach dwóch prezentówJulce zostało \(0,45x\) oszczędności, więc zostało jej \(45\%\).
- Odpowiedź:
C. \(45\)
6. Obniżki/podwyżki
Podpowiedź: Druga obniżka/podwyżka następuje z ceny już obniżonej/podwyższonej, a nie z ceny początkowej.
Ostatnia deska ratunku: Możemy sobie założyć że nasz produkt na starcie kosztuje nie \(x\), tylko \(100zł\). To znacznie upraszcza późniejsze dostrzeżenie tego jaka jest wysokość obniżki/podwyżki lub rabatu.
- Rozwiązanie:
Krok 1. Obliczenie wysokości obniżki.
$$220zł-176zł=44zł$$
Krok 2. Obliczenie o ile procent obniżono cenę butów.Cenę obniżono o \(44zł\) z \(220zł\), czyli:
$$\frac{44}{220}\cdot100\%=\frac{1}{5}\cdot100\%=20\%$$ - Odpowiedź:
B. \(20\)
- Rozwiązanie:
Tego typu zadania możemy rozwiązać na dwa sposoby.Sposób I – rozwiązanie na konkretnych liczbach:Krok 1. Obliczenie wysokości pierwszej obniżki.Pierwsza obniżka jest o \(10\%\) z \(30000zł\), zatem wynosi ona:
$$0,1\cdot30000zł=3000zł$$Krok 2. Obliczenie ceny samochodu po pierwszej obniżce.$$30000zł-3000zł=27000zł$$
Krok 3. Obliczenie wysokości drugiej obniżki.Nasza druga obniżka jest także o \(10\%\), ale tym razem już z \(27000zł\), zatem wynosi ona:
$$0,1\cdot27000zł=2700zł$$Krok 4. Obliczenie ceny samochodu po drugiej obniżce.$$27000zł-2700zł=24300zł$$
Sposób II – rozwiązanie na wyrażeniach algebraicznych (metoda bardziej uniwersalna):Krok 1. Obliczenie ceny samochodu po pierwszej obniżce.Oznaczmy cenę samochodu jako \(x\) i obliczmy wartość samochodu po pierwszej obniżce. Skoro obniżka jest o \(10\%\), to nowa cena stanowi teraz \(90\%\) ceny podstawowej. Cena samochodu po pierwszej obniżce jest więc równa \(0,9x\).
Krok 2. Obliczenie ceny samochodu po drugiej obniżce.Ceną wyjściową jest dla nas teraz \(0,9x\) i to od tej ceny ponownie odejmujemy \(10\%\), czyli cena samochodu po drugiej obniżce będzie równa:
$$0,9\cdot0,9x=0,81x$$Cena samochodu po dwóch obniżkach stanowi więc \(0,81\) ceny podstawowej (czyli \(81\%\)). Chcąc poznać nową cenę wystarczy teraz pomnożyć \(0,81\) przez początkową cenę samochodu.
$$0,81\cdot30000zł=24300zł$$ - Odpowiedź:
D. \(24300zł\)
7. Błąd bezwzględny/względny
Podpowiedź: Wzorów na błąd bezwzględny i względny nie znajdziemy w tablicach, to jedna z tych rzeczy którą musimy nauczyć się na pamięć. Te wzory znajdziesz tutaj: Błąd bezwzględny i względny
Ostatnia deska ratunku: Tak na chłopski rozum, to błąd bezwzględny mówi konkretnie o ile się pomyliliśmy. Przykładowo jak masz 178cm wzrostu, a ktoś szacuje że masz 180cm, to błąd bezwzględny jest równy 2cm. Jeżeli więc na maturze będzie jakieś zadanie z niewiadomą \(x\), to może uda Ci się wprowadzić sensowny kontekst do tego zadania tak jak np. ze wzrostem i dzięki temu łatwiej będzie obliczać różne rzeczy.
- Rozwiązanie:
Aby obliczyć błąd względny musimy posłużyć się następującym wzorem:
$$δ=\frac{|x-x_{o}|}{x}$$W naszym przykładzie:
$$x=\frac{5}{8}=0,625 \\
x_{o}=0,6 \\
\text{więc} \\
δ=\frac{|0,625-0,6|}{0,625} \\
δ=\frac{0,025}{0,625} \\
δ=0,04=4\%$$ - Odpowiedź:
D. \(4\%\)
- Rozwiązanie:
Liczba \(15\) jest przybliżeniem z niedomiarem, czyli na pewno poszukiwana przez nas liczba \(x\) jest większa od \(15\). Skoro więc błąd bezwzględny wyniósł \(0,24\), to nasza liczba \(x\) jest równa:
$$x=15+0,24=15,24$$ - Odpowiedź:
D. \(15,24\)
8. Ile rozwiązań ma równanie/nierówność lub jaka jest największa/najmniejsza liczba spełniająca równanie/nierówność.
Podpowiedź: Zwróć uwagę na to, czy jakiegoś otrzymanego rozwiązania nie trzeba wykluczyć (np. ze względu na założenia).
Ostatnia deska ratunku: Jak pytają się nas jaka jest największa/najmniejsza liczba spełniająca równanie lub nierówność, to możemy podstawiać każdą z odpowiedzi do naszego działania i w ten sposób sprawdzimy kiedy równanie lub nierówność jest prawidłowe.
- Rozwiązanie:
Krok 1. Pozbycie się ułamków i rozwiązanie nierówności.
Przy równościach i nierównościach w których dominują ułamki dobrze jest na samym początku pomnożyć obie strony przez taką liczbę, aby pozbyć się wszystkich ułamków. W naszym przypadku taką liczbą będzie \(24\), bo jest to najmniejsza wspólna wielokrotność \(6,8,12\). Jak już to zrobimy, to bez przeszkód obliczymy naszą nierówność:
$$\frac{3}{8}+\frac{x}{6}\lt\frac{5x}{12} \quad\bigg/\cdot24 \\
9+4x\lt10x \\
9\lt6x \\
x\gt\frac{9}{6} \\
x\gt\frac{3}{2}$$Krok 2. Wybór prawidłowej odpowiedzi.Rozwiązaniem naszej nierówności jest zbiór liczb rzeczywistych większych od \(\frac{3}{2}\). To oznacza, że najmniejszą liczbą całkowitą spełniającą tę nierówność jest \(2\).
- Odpowiedź:
B. \(2\)
- Rozwiązanie:
Aby sprawdzić ile rozwiązań ma dane równanie spróbujmy je rozwiązać tradycyjnymi metodami:
$$\frac{3x-1}{x+5}=3 \quad\bigg/\cdot(x+5) \\
3x-1=3\cdot(x+5) \\
3x-1=3x+15 \\
-1=15$$Otrzymaliśmy sprzeczność, a to oznacza, że to równanie nie ma rozwiązań rzeczywistych.
- Odpowiedź:
A. nie ma rozwiązań rzeczywistych
9. Układ równań
Podpowiedź: Czasem w układzie równań znajdziemy wzory dwóch prostych. W takich przypadkach rozwiązaniem układu równań jest miejsce przecięcia się tych prostych (jest to tak zwana geometryczna interpretacja układu równań).
Ostatnia deska ratunku: Możemy podstawiać poszczególne odpowiedzi do układu równań, sprawdzając która odpowiedź jest prawidłowa. Jak ma to być standardowy układ równań gdzie rozwiązaniem jest para liczb, to po podstawieniu iksa i igreka lewa i prawa strona każdego z równań musi być sobie równa. Jak układ ma być tożsamościowy (czyli ma mieć nieskończenie wiele rozwiązań) to po podstawieniu powinno nam wyjść coś w stylu \(1=1\), \(3=3\) itd. Jak układ ma być sprzeczny (czyli ma mieć zero rozwiązań), to musi wychodzić nam sprzeczność typu \(1=3\).
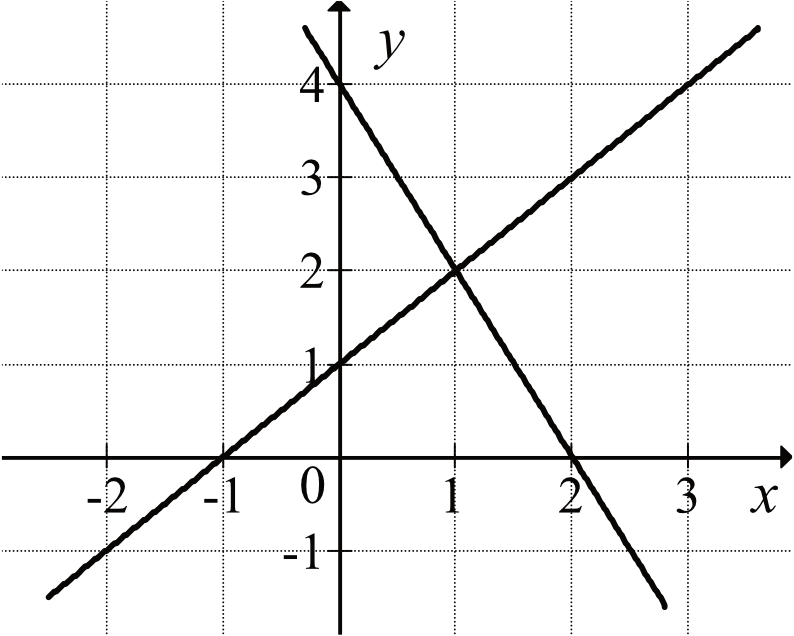
Wskaż ten układ.
y=x+1 \\
y=-2x+4
\end{cases}\)
y=x-1 \\
y=2x+4
\end{cases}\)
y=x-1 \\
y=-2x+4
\end{cases}\)
y=x+1 \\
y=2x+4
\end{cases}\)
- Rozwiązanie:
Wszystkie proste przedstawione są w postaci \(y=ax+b\), a naszym zadaniem jest tak naprawdę odczytanie z rysunku potrzebnych informacji i ustalenie poszczególnych współczynników \(a\) oraz \(b\).Krok 1. Ustalenie wzoru pierwszej prostej (rosnącej).Jeśli przyjrzymy się odpowiedziom to pierwsza prosta jest przedstawiona w dwóch wariantach: \(y=x+1\) lub \(y=x-1\). Musimy więc tak naprawdę ustalić współczynnik \(b\) tej prostej i dowiedzieć się, czy jest on równy \(1\), czy \(-1\). Współczynnik \(b\) mówi nam o tym w którym miejscu z osią \(Oy\) przetnie się wykres prostej. W naszym przypadku przeciął się on w punkcie \((0;1)\), a więc \(b=1\). To oznacza, że pierwsza prosta ma na pewno postać \(y=x+1\).
Krok 2. Ustalenie wzoru drugiej prostej (malejącej).Druga prosta jest opisana w odpowiedziach na dwa sposoby: \(y=2x+4\) lub \(y=-2x+4\). To znaczy, że musimy tym razem zweryfikować wartość współczynnika \(a\) i stwierdzić, czy jest on równy \(2\), czy może \(-2\). Skoro prosta jest malejąca, to bez żadnych zbędnych obliczeń jesteśmy w stanie stwierdzić, że prosta jest malejąca, czyli \(a=-2\).
Przy okazji widzimy też, że współczynnik \(b=4\), bo prosta ta przecina oś \(Oy\) w punkcie \((0;4)\), więc z całą pewnością wzorem tej prostej jest \(y=-2x+4\).To oznacza, że poszukiwanym przez nas układem jest ten z pierwszej odpowiedzi.
- Odpowiedź:
A. \(\begin{cases}
y=x+1 \\
y=-2x+4
\end{cases}\)
4x+2y=10 \\
6x+ay=15
\end{cases}\) ma nieskończenie wiele rozwiązań, jeśli:
- Rozwiązanie:
Aby układ równań miał nieskończenie wiele rozwiązań to pierwsze i drugie równanie musimy doprowadzić do identycznej postaci, dzięki czemu bez problemu wyznaczymy parametr \(a\):
\begin{cases}
4x+2y=10 \quad\bigg/\cdot1,5 \\
6x+ay=15
\end{cases}\begin{cases}
6x+\color{blue}{3y}=15 \\
6x+\color{blue}{ay}=15
\end{cases}Skoro w pierwszym równaniu pojawiła nam się wartość \(3y\), to parametr \(a\) w drugim równaniu także musi być równy \(3\).
- Odpowiedź:
D. \(a=3\)
10. Rozwiązywanie równań kwadratowych
Podpowiedź: Jeżeli chcemy rozwiązać równanie kwadratowe za pomocą delty, to musimy mieć postać ogólną. W związku z tym jeśli mamy równanie typu \(2x^2-3x=5\), to najpierw musimy je przekształcić do postaci \(2x^2-3x-5=0\). Oczywiście nie trzeba zawsze na siłę doprowadzać równania do postaci ogólnej – jak mamy postać iloczynową, to wystarczy przyrównać wartości w nawiasach do zera. I jeszcze jedna ważna uwaga – często rozwiązania równań nazywa się „pierwiastkami równania”.
Ostatnia deska ratunku: Jak rozwiążesz równanie, to sprawdź zawsze czy otrzymane rozwiązanie w ogóle spełnia to równanie (czyli podstaw wyznaczonego iksa i zobacz, czy lewa i prawa strona równania będą sobie równe).
- Rozwiązanie:
Krok 1. Obliczenie rozwiązań równania kwadratowego.
W treści zadania mamy tak naprawdę podane równanie kwadratowe w postaci iloczynowej. To oznacza, że wystarczy przyrównać wartości z poszczególnych nawiasów do zera i dzięki temu poznamy rozwiązania tego równania, tak więc:
$$x+2=0 \quad\lor\quad x-6=0 \\
x=-2 \quad\lor\quad x=6$$Równanie ma więc dwa rozwiązania: \(x_{1}=-2\) oraz \(x_{2}=6\).
Krok 2. Obliczenie wartości \({x_{1}}^2+{x_{2}}^2\).$${x_{1}}^2+{x_{2}}^2=(-2)^2+6^2=4+36=40$$
- Odpowiedź:
C. \(40\)
- Rozwiązanie:
Krok 1. Obliczenie delty.
Współczynniki: \(a=2,\;b=11,\;c=3\)
$$Δ=b^2-4ac=11^2-4\cdot2\cdot3=121-24=97$$Delta wyszła nam dodatnia, więc równanie ma na pewno dwa rozwiązania. Musimy jeszcze tylko ustalić czy są to rozwiązania dodatnie, czy też ujemne.
Krok 2. Określenie, czy rozwiązania są dodatnie czy ujemne.Najprościej będzie określić znak obliczając po prostu wartości \(x_{1}\) oraz \(x_{2}\):
$$\sqrt{Δ}=\sqrt{97}\approx9,8$$$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-11-9,8}{2\cdot2}=\frac{-20,8}{4}=-5,2 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-11+9,8}{2\cdot2}=\frac{-1,2}{4}=-0,3$$ - Odpowiedź:
D. ma dwa ujemne rozwiązania rzeczywiste.
11. Rozwiązywanie nierówności kwadratowych
Podpowiedź: Podczas rozwiązywania nierówności kwadratowych musimy na początku rozwiązać równanie kwadratowe i robimy to po to, by wyznaczyć miejsca zerowe. W związku z tym jak w trakcie rozwiązywania otrzymamy ujemną deltę, to nie oznacza to że nierówność nie ma rozwiązań. Oznacza to tylko tyle, że parabola nie ma miejsc zerowych (czyli w całości jest nad osią lub pod osią iksów).
Ostatnia deska ratunku: I tu podobnie jak w równaniach kwadratowych, tak i tutaj możemy sprawdzać czy otrzymane rozwiązanie ma sens. Najlepiej jest tutaj podstawić sobie jakieś krańcowe liczby z otrzymanego przedziału rozwiązań.
- Rozwiązanie:
Krok 1. Zapisanie nierówności w postaci ogólnej.
To bardzo ważny krok. Jeśli chcemy rozwiązać to zadanie np. metodą delty, to musimy doprowadzić nierówność do postaci typu \(ax^2+bx+c\), tak aby po prawej stronie znalazło się zero. Stąd też pierwszą czynnością jaką musimy zrobić to wymnożyć przez siebie odpowiednie nawiasy i uporządkować zapis:
$$2x^2-4x\gt(x+3)(x-2) \\
2x^2-4x\gt x^2-2x+3x-6 \\
x^2-5x+6\gt0$$Krok 2. Obliczenie miejsc zerowych wielomianu.Współczynniki: \(a=1,\;b=-5,\;c=6\)
$$Δ=b^2-4ac=(-5)^2-4\cdot1\cdot6=25-24=1 \\
\sqrt{Δ}=\sqrt{1}=1$$$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-5)-1}{2\cdot1}=\frac{5-1}{2}=\frac{4}{2}=2 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-5)+1}{2\cdot1}=\frac{5+1}{2}=\frac{6}{2}=3$$Krok 3. Szkicowanie wykresu paraboli.Współczynnik \(a\) był dodatni, więc parabola będzie mieć ramiona skierowane do góry. Zaznaczamy na osi wyliczone przed chwilą miejsca zerowe (z pustymi kropkami, bo w nierówności wystąpił znak \(\gt\)).

Szukamy argumentów dla których funkcja przyjmuje wartości dodatnie, a więc interesującym nas przedziałem będzie:
$$x\in(-\infty;2)\cup(3;+\infty)$$ - Odpowiedź:
\(x\in(-\infty;2)\cup(3;+\infty)\)
- Rozwiązanie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Nasza nierówność przedstawiona jest w postaci iloczynowej, tak więc bardzo szybko jesteśmy w stanie określić miejsca zerowe – wystarczy przyrównać poszczególne wartości w nawiasach do zera.
$$(2x-3)(3-x)=0 \\
2x-3=0 \quad\lor\quad 3-x=0 \\
2x=3 \quad\lor\quad x=3 \\
x=1\frac{1}{2} \quad\lor\quad x=3$$Krok 2. Szkicowanie wykresu paraboli.Musimy teraz określić kształt naszej paraboli. Gdybyśmy pomnożyli przez siebie wszystkie czynniki to otrzymalibyśmy między innymi \(-2x^2\), tak więc współczynnik kierunkowy \(a\) wyjdzie nam ujemny. To z kolei oznacza, że ramiona paraboli będą skierowane do dołu. Zaznaczmy więc na osi wyznaczone przed chwilą miejsca zerowe (kropki będą zamalowane, bo w nierówności wystąpił znak \(\ge\)) i na podstawie wykresu określmy przedział rozwiązań podanej nierówności.

Szukamy argumentów dla których funkcja przyjmuje wartości dodatnie, a więc interesującym nas przedziałem będzie: \(x\in\langle1\frac{1}{2};3\rangle\).
- Odpowiedź:
\(x\in\langle1\frac{1}{2};3\rangle\)
12. Odczytywanie informacji z wykresu funkcji (głównie funkcji liniowej lub kwadratowej)
Podpowiedź: Tutaj możemy otrzymać jakiś skomplikowany wykres z którego trzeba będzie odczytać np. zbiór argumentów (odczytujemy to z osi iksów) lub zbiór wartości (odczytujemy z osi igreków). Ale oprócz tego, to często zadania z odczytywaniem informacji z wykresu oparte są na tym, by odczytać jakąś kluczową informację z wykresu funkcji liniowej lub kwadratowej. Dla funkcji liniowych kluczowe zazwyczaj będzie odczytanie miejsca zerowego i tego czy funkcja jest rosnąca, czy malejąca. Dla funkcji kwadratowych ważne są miejsca zerowe, wierzchołek paraboli, czy też kierunek ułożenia ramion.
Ostatnia deska ratunku: Próbuj odrzucać jakieś odpowiedzi ze względu na informacje, które potrafisz odczytać z wykresu. Jak przykładowo szukamy wzoru funkcji liniowej, a widzisz że funkcja jest rosnąca, to możesz odrzucić te funkcje, które mają ujemny współczynnik kierunkowy.
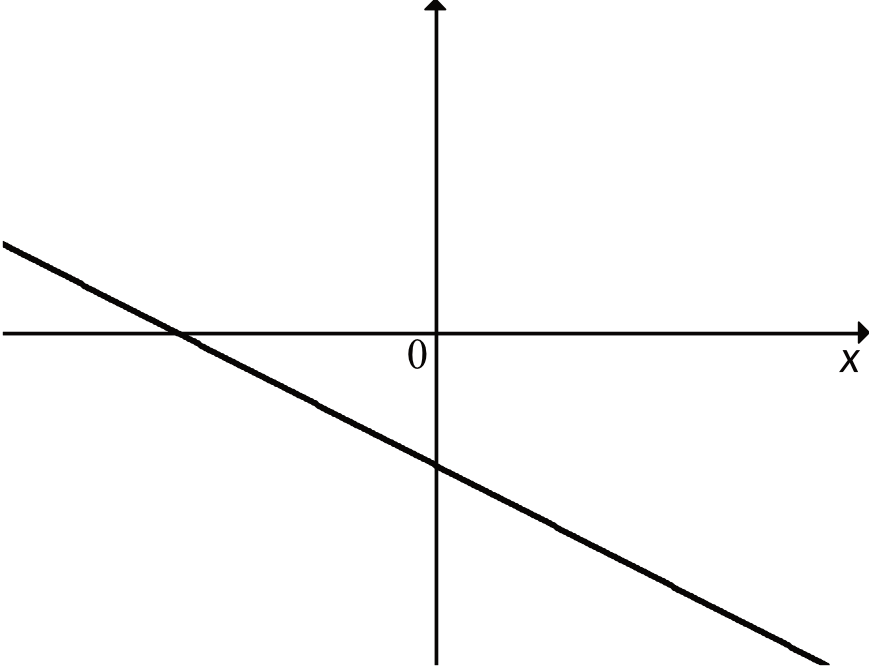
Jakie znaki mają współczynniki \(a\) i \(b\)?
- Rozwiązanie:
Krok 1. Ustalenie wartości współczynnika \(a\).
Z wykresu możemy odczytać, że funkcja jest malejąca, a to oznacza, że \(a\lt0\).
Krok 2. Ustalenie wartości współczynnika \(b\).Współczynnik \(b\) wskazuje nam w którym miejscu wykres funkcji \(y=ax+b\) przecina się z osią \(Oy\). Przykładowo gdy \(b=-2\), to wykres przecina oś w miejscu \(A=(0,-2)\). Widzimy wyraźnie, że nasza funkcja przecina oś \(Oy\) pod osią \(Ox\), a więc, a więc \(b\lt0\).
- Odpowiedź:
A. \(a\lt0\) i \(b\lt0\)
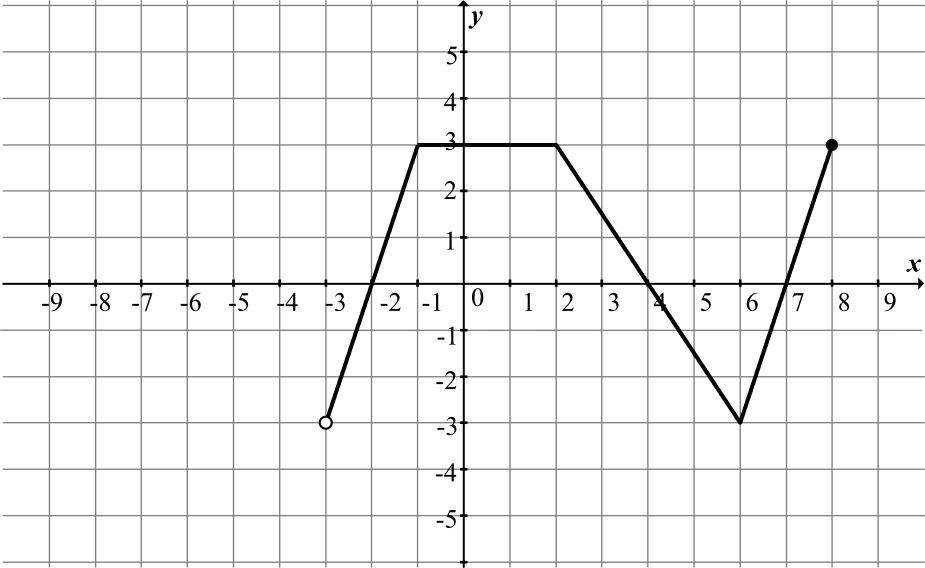
- Rozwiązanie:
Dziedzinę funkcji odczytujemy z osi \(x\). Widzimy wyraźnie, że dziedziną funkcji będzie przedział \(x\in(-3;8\rangle\). - Odpowiedź:
D. \((-3,8\rangle\)
13. Punkt należący do funkcji oraz obliczanie wartości funkcji
Podpowiedź: Punkt należy do funkcji wtedy, gdy podstawiając jego współrzędne do wzoru funkcji, lewa i prawa strona równania będą sobie równe.
Ostatnia deska ratunku: No i właśnie, czasem podstawiając współrzędne danego punktu do wzoru funkcji możemy wykluczyć jakąś odpowiedź lub też możemy sprawdzić, czy w zadaniu otwartym wyszedł nam dobry wynik. Jak np. szukamy funkcji przechodzącej przez jakiś punkt, to warto podstawić współrzędne tego punktu do otrzymanego wzoru i sprawdzić, czy obie strony równania będą sobie równe.
- Rozwiązanie:
Zadanie możemy rozwiązać podstawiając współrzędne każdego z punktów do wzoru funkcji. Pierwszą współrzędną podstawiamy w miejsce \(x\), a drugą w miejsce \(f(x)\). Punktem należącym do wykresu będzie ten, który spełni powstałą równość (czyli tak naprawdę wtedy kiedy nie wyjdzie nam równanie sprzeczne).Można jednak to zadanie zrobić nieco sprytniej, dostrzegając że we wszystkich odpowiedziach pierwszą współrzędną punktu jest \(x=-1\). To oznacza, że nie musimy podstawiać każdego z punktów pod wzór funkcji. Wystarczy tak naprawdę obliczyć wartość \(f(-1)\), zatem:
$$f(-1)=(-1)^2+(-1)-2 \\
f(-1)=1-1-2 \\
f(-1)=-2$$To oznacza, że druga współrzędna to \(y=-2\), czyli prawidłowa jest ostatnia odpowiedź \((-1;-2)\).
- Odpowiedź:
D. \((-1,-2)\)
- Rozwiązanie:
Aby obliczyć wartość \(f(\sqrt{2})\) wystarczy tak naprawdę podstawić \(x=\sqrt{2}\), zatem:
$$f(\sqrt{2})=\frac{2\cdot\sqrt{2}-8}{\sqrt{2}}$$Nie możemy skrócić ot tak pierwiastków, bo w liczniku mamy odejmowanie. Można za to pokusić się o np. usunięcie niewymierności z mianownika:
$$f(\sqrt{2})=\frac{2\sqrt{2}}{\sqrt{2}}-\frac{8}{\sqrt{2}} \\
f(\sqrt{2})=\frac{2\sqrt{2}\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}-\frac{8\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
f(\sqrt{2})=\frac{2\cdot2}{2}-\frac{8\sqrt{2}}{2} \\
f(\sqrt{2})=2-4\sqrt{2}$$ - Odpowiedź:
A. \(2-4\sqrt{2}\)
14. Miejsce zerowe funkcji
Podpowiedź: Miejsce zerowe \(x=2\) oznacza, że funkcja na pewno przechodzi przez punkt \(P=(2;0)\).
Ostatnia deska ratunku: Gdy szukamy miejsca zerowego funkcji, to nie podstawiamy pod iksa wartości równej zero, tylko przyrównujemy wzór funkcji do zera. Przykładowo aby wyznaczyć miejsce zerowe funkcji \(y=2x+3\) to sprawdzamy kiedy \(2x+3=0\). Poza tym miejsca zerowe odczytujemy z osi iksów, a nie z igreków. Często właśnie to jest główna pułapka w zadaniu. Możesz więc śmiało odrzucać odpowiedzi, gdzie miejsca zerowe odczytywane są z osi igreków.
- Rozwiązanie:
Miejscem zerowym funkcji jest taki argument \(x\) dla którego cała funkcja przyjmuje wartość równą zero. To oznacza, że miejsce zerowe wyliczymy w następujący sposób:
$$-\sqrt{2}x+4=0 \\
-\sqrt{2}x=-4 \\
\sqrt{2}x=4 \quad\bigg/:\sqrt{2} \\
x=\frac{4}{\sqrt{2}}=\frac{4\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$$ - Odpowiedź:
D. \(2\sqrt{2}\)
- Rozwiązanie:
Mamy podaną funkcję kwadratową w postaci iloczynowej. Aby obliczyć jej miejsca zerowe wystarczy przyrównać wzór tej funkcji do zera. Pamiętaj, że iloczyn będzie równy zero tylko i wyłącznie wtedy, gdy jeden z czynników (czyli jeden z nawiasów) będzie równy zero. Stąd też:
$$-3(x-7)(x+2)=0 \\
x-7=0 \quad\lor\quad x+2=0 \\
x=7 \quad\lor\quad x=-2$$ - Odpowiedź:
A. \(x=7,\;x=-2\)
15. Współczynniki i wzory funkcji liniowej/kwadratowej
Podpowiedź: W funkcji liniowej \(y=ax+b\) i kwadratowej \(y=ax^2+bx+c\) kluczowy jest współczynnik kierunkowy \(a\). Gdy funkcja liniowa rośnie, to \(a\gt0\), gdy maleje to \(a\lt0\), a gdy jest stała to \(a=0\). W przypadku funkcji kwadratowej gdy ramiona paraboli są skierowane do góry to \(a\gt0\), a gdy do dołu to \(a\lt0\). W funkcji kwadratowej często też kluczowe będzie wyznaczenie wierzchołka paraboli (pamiętaj, że \(p=\frac{-b}{2a}\) oraz \(q=\frac{-Δ}{4a}\)).
Ostatnia deska ratunku: Jak rozwiązujemy jakieś zadanie gdzie trzeba wyznaczyć wzór funkcji, to sprawdźmy sobie na koniec czy nasz otrzymany wynik ma sens – np. jak funkcja jest rosnąca to sprawdźmy czy wyszedł nam dodatni współczynnik kierunkowy. Warto też podstawić współrzędne znanego nam punktu do tego wzoru – sprawdzimy w ten sposób, czy lewa i prawa strona są sobie równe.
- Rozwiązanie:
Krok 1. Ustalenie, czy funkcja \(f(x)\) jest rosnąca czy malejąca.
O tym, czy funkcja jest rosnąca czy malejąca decyduje współczynnik \(a\) stojący przed \(x\). W naszym przypadku współczynnik ten jest dodatni i wynosi \(\frac{1}{2}\), a więc już wiemy, że funkcja jest rosnąca.
Krok 2. Ustalenie przez jaki punkt przechodzi wykres funkcji.W tym przypadku pomocny będzie współczynnik \(b\), który w naszym przypadku jest równy \(b=-6\). Mówi on o tym, że wykres funkcji przecina oś \(Oy\) w punkcie \((0;-6)\).
To oznacza, że prawidłowa jest ostatnia odpowiedź.
- Odpowiedź:
D. Jest rosnąca i jej wykres przechodzi przez punkt \((0,-6)\)
- Rozwiązanie:
Krok 1. Obliczenie pierwszej współrzędnej wierzchołka (\(p\)).
Do obliczeń współrzędnych wierzchołka \(W=(p;q)\) przydadzą nam się współczynniki funkcji kwadratowej:
$$a=1,\;b=-4,\;c=4$$Zgodnie ze wzorami z tablic matematycznych:
$$p=\frac{-b}{2a} \\
p=\frac{-(-4)}{2\cdot1} \\
p=\frac{4}{2} \\
p=2$$Tak naprawdę moglibyśmy już na tym skończyć obliczenia, bo już wiemy, że współrzędne naszego wierzchołka to \(W=(2;q)\), a taka sytuacja jest jedynie w czwartej odpowiedzi. W ramach ćwiczenia możemy obliczyć jeszcze drugą współrzędną.
Krok 2. Obliczenie drugiej współrzędnej wierzchołka.$$Δ=b^2-4ac=(-4)^2-4\cdot1\cdot4=16-16=0$$
$$q=\frac{-Δ}{4a} \\
q=\frac{-0}{4\cdot1}\\
q=\frac{-0}{4}\\
q=0$$Współrzędne wierzchołka to w takim razie \(W=(2;0)\).
- Odpowiedź:
D. \((2,0)\)
16. Najmniejsza/największa wartość funkcji (także w konkretnym przedziale)
Podpowiedź: Ogólnie funkcja kwadratowa przyjmuje największą lub najmniejszą wartość w swoim wierzchołku. I to dość ważne, bo czasem powiedzą nam w treści zadania, że funkcja ma jakąś tam największą lub najmniejszą wartość i my powinniśmy wyciągnąć z tego wniosek, że to będzie po prostu wierzchołek. Może też być tak, że trzeba będzie wyliczyć najmniejszą lub największą wartość w danym przedziale – wtedy ta najmniejsza/największa wartość przyjmowana jest albo na krańcach przedziału albo w wierzchołku (o ile wierzchołek znajduje się w tym przedziale).
Ostatnia deska ratunku: Można spróbować narysować wskazaną funkcję i przedział, próbując odczytać z takiego wykresu gdzie ta wartość najmniejsza lub największa się znajduje.
- Rozwiązanie:
Funkcja będzie przyjmować największą i najmniejszą wartość w danym przedziale albo na krańcach tego przedziału albo w punkcie, który jest wierzchołkiem funkcji. Wartości krańcowe przedziałów są nam znane, więc potrzebujemy jeszcze wyznaczyć położenie wierzchołka (wystarczy nam jego współrzędna \(x\)).Krok 1. Wyznaczenie współrzędnej \(x\) wierzchołka paraboli.Współrzędną wierzchołka paraboli \(x_{W}\) dla funkcji określonej wzorem w postaci \(ax^2+bx+c\) obliczymy w następujący sposób:
$$x_{W}=\frac{-b}{2a}=\frac{-(-6)}{2\cdot1}=\frac{6}{2}=3$$Sprawdzamy teraz, czy wierzchołek w ogóle znajduje się w naszym przedziale, który mamy przeanalizować. Tak się składa, że \(x=3\) mieści się w przedziale \(\langle0;4\rangle\), więc jak najbardziej uwzględnimy go w naszych obliczeniach.
Krok 2. Obliczenie wartości \(f(0)\), \(f(4)\) oraz \(f(3)\).Zgodnie z tym co napisaliśmy sobie na początku, największych i najmniejszych wartości zawsze spodziewamy się na krańcach przedziału albo w punkcie który jest wierzchołkiem. Sprawdźmy więc jakie wartości przyjmuje ta funkcja dla tych trzech argumentów, a następnie wybierzemy z nich najmniejszą i największą wartość.
$$f(0)=0^2-6\cdot0+3=0-0+3=3 \\
f(4)=4^2-6\cdot4+3=16-24+3=-5 \\
f(3)=3^2-6\cdot3+3=9-18+3=-6$$Najmniejszą wartością tej funkcji w przedziale \(\langle0;4\rangle\) jest więc \(-6\) (dla \(x=3\)), a największą jest \(3\) (dla \(x=0\)).
- Odpowiedź:
Najmniejszą wartością jest \(-6\). Największą wartością jest \(3\).
- Rozwiązanie:
Krok 1. Ustalenie współrzędnych wierzchołka paraboli.
Bardzo ważną informacją jest to, że dla \(x=-3\) funkcja przyjmuje wartość \(y=4\), która jest jednocześnie najwyższą wartością tej funkcji. Krótko mówiąc – jest to po prostu wierzchołek paraboli. Tak więc \(W=(-3;4)\).
Krok 2. Zapisanie wzoru funkcji w postaci kanonicznej.Znając współrzędne wierzchołka możemy zapisać wzór funkcji kwadratowej w następującej postaci:
$$f(x)=a(x-p)^2+q$$gdzie \(p\) i \(q\) są współrzędnymi wierzchołka paraboli.
Tak więc nasza funkcja przyjmuje wzór:
$$f(x)=a(x-(-3))^2+4 \\
f(x)=a(x+3)^2+4$$Krok 3. Wyznaczenie współczynnika \(a\) i ostatecznego wzoru funkcji.Znamy już prawie pełny wzór naszej funkcji, brakuje nam jeszcze współczynnika \(a\).
Tak na marginesie, to jeśli dobrze sobie wyobrazimy tę sytuację, to już powinniśmy wiedzieć, że na pewno będzie on ujemny. Skąd to wiadomo? Skoro funkcja przyjmuje najwyższe wartości w swoim wierzchołku to jej ramiona muszą być skierowane do dołu, a więc \(a\lt0\). Gdyby ramiona były skierowane do góry, to najwyższą wartością byłoby \(+\infty\).
Do obliczenia wartości współczynnika \(a\) wykorzystamy punkt \(A=(-1,3)\), który należy do wykresu tej funkcji. Podstawiamy jego współrzędne do wzoru wyznaczonego w poprzednim kroku i otrzymujemy:
$$f(x)=a(x+3)^2+4 \\
3=a(-1+3)^2+4 \\
-1=a\cdot2^2 \\
-1=4a \\
a=-\frac{1}{4}$$Poszukiwanym wzorem funkcji kwadratowej jest więc \(f(x)=-\frac{1}{4}(x+3)^2+4\).
Oczywiście moglibyśmy jeszcze wykonać potęgowanie (choć nie jest to już konieczne) i wtedy otrzymalibyśmy postać ogólną:
$$f(x)=-\frac{1}{4}(x^2+6x+9)+4 \\
f(x)=-\frac{1}{4}x^2-\frac{6}{4}x-\frac{9}{4}+4 \\
f(x)=-\frac{1}{4}x^2-\frac{3}{2}x+\frac{7}{4}$$ - Odpowiedź:
\(f(x)=-\frac{1}{4}(x+3)^2+4\) lub zapisując to w postaci ogólnej \(f(x)=-\frac{1}{4}x^2-\frac{3}{2}x+\frac{7}{4}\)
17. Przekształcanie funkcji
Podpowiedź: Najtrudniejsze są przesunięcia w prawo/lewo, bo są one dość nieintuicyjne. Jeśli funkcję \(f(x)\) przesuwamy w prawo, to nasza nowa funkcja ma wzór typu \(g(x)=f(x-1)\) (czyli z minusem wewnątrz), a gdy przesuwamy ją w lewo to możemy mieć wzór typu \(h(x)=f(x+1)\) (czyli z plusem wewnątrz).
Ostatnia deska ratunku: Jak są podane jakieś rysunki, a my szukamy wzoru przekształconej funkcji, podstawmy sobie do wzorów z odpowiedzi ABCD np. \(x=1\), \(x=2\) i zobaczmy jaką wartość przyjmie funkcja dla takich argumentów. Wtedy będziemy mogli sprawdzić, czy otrzymana wartość jest pokazana także na wykresie.
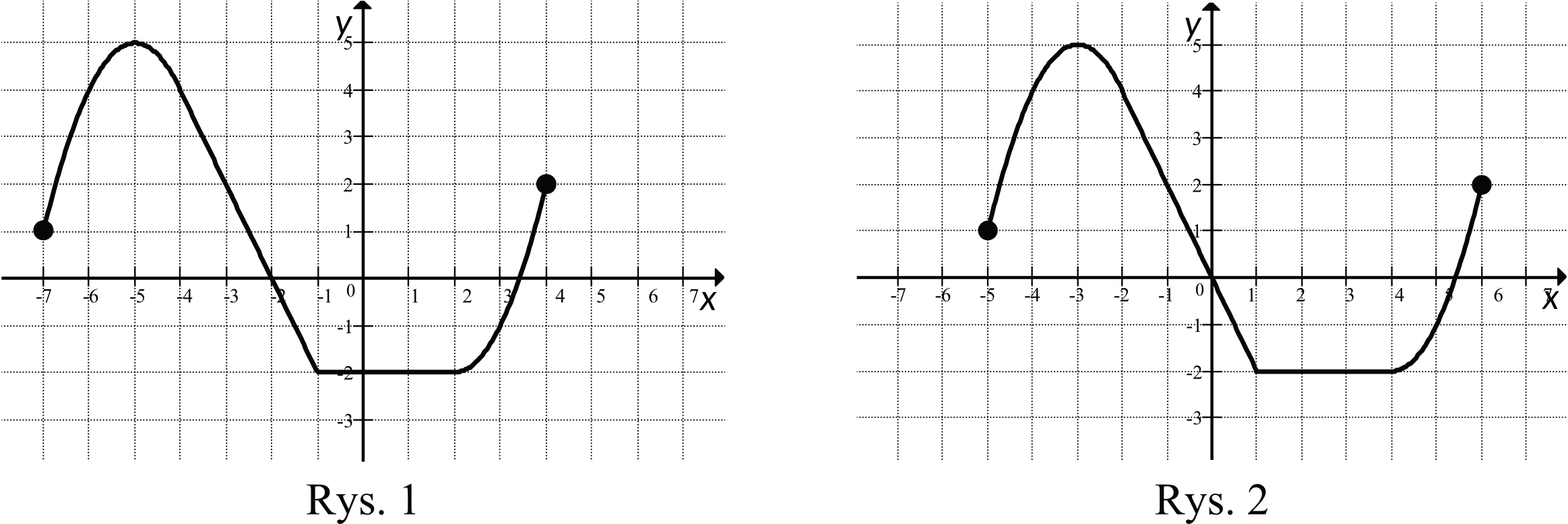
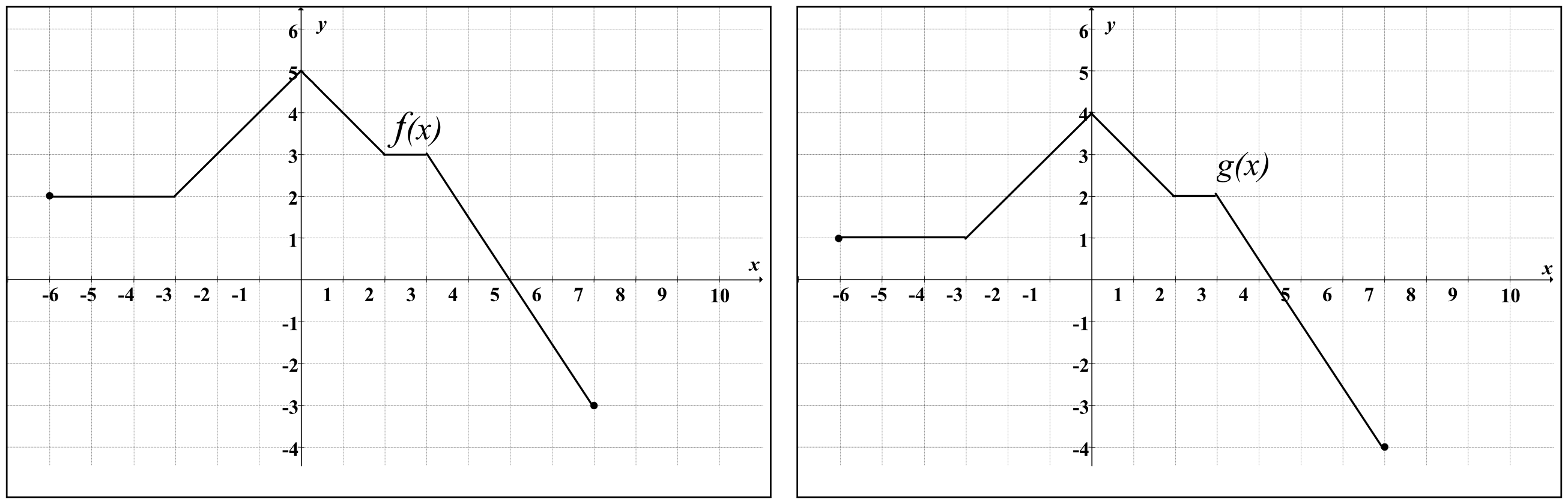
Rysunek 2 przedstawia wykres funkcji:
- Rozwiązanie:
Wykres funkcji z drugiego rysunku jest przesunięty o dwie jednostki w prawo względem wykresu funkcji z rysunku pierwszego.
To oznacza, że prawidłowym wzorem wykresu drugiej funkcji będzie ten w którym wartość argumentu \(x\) jest pomniejszona o \(2\), czyli \(y=f(x-2)\). - Odpowiedź:
C. \(y=f(x-2)\)
- Rozwiązanie:
Wykres funkcji \(g\) jest przesunięciem funkcji \(f\) o jedno miejsce w dół, zatem:
$$g(x)=f(x)-1$$ - Odpowiedź:
B. \(g(x)=f(x)-1\)
18. Wyznaczanie wartości jakiegoś wyrazu ciągu arytmetycznego/geometrycznego
Podpowiedź: Zdarza się, że kluczową informacją jest to, że ciąg jest rosnący/malejący/niemonotoniczny. Może to być powód dla którego któreś z otrzymanych rozwiązań trzeba odrzucić. Dlatego też jak otrzymamy dwa możliwe wyniki (a w ciągach geometrycznych często tak właśnie będzie, bo będą tam się pojawiać równania kwadratowe) to sprawdźmy zawsze jak zachowuje się ciąg dla pierwszego i drugiego rozwiązania.
Ostatnia deska ratunku: Próbujmy rozpisywać kolejne wyrazy ciągu, może w ten ręczny sposób dojdziemy do tego czego poszukujemy.
- Rozwiązanie:
Wartość pierwszego wyrazu obliczymy korzystając ze wzoru na \(n\)-ty wyraz ciągu arytmetycznego, w którym znajduje się poszukiwana przez nas wartość \(a_{1}\):
$$a_{n}=a_{1}+(n-1)r \\
a_{20}=a_{1}+(20-1)r \\
17=a_{1}+19\cdot(-2) \\
17=a_{1}-38 \\
a_{1}=55$$ - Odpowiedź:
C. \(55\)
- Rozwiązanie:
Krok 1. Wyznaczenie wartości ilorazu \(q\).
Znając wartości dwóch kolejnych wyrazów ciągu geometrycznego (czyli \(a_{1}\) oraz \(a_{2}\)) możemy wyznaczyć wartość \(q\) z następującego wzoru:
$$q=\frac{a_{2}}{a_{1}} \\
q=\frac{a_{2}}{a_{1}} \\
q=\frac{12}{2}=6$$Krok 2. Wyznaczenie wartości czwartego wyrazu ciągu geometrycznego.Znając wartość \(a_{1}\) oraz \(q\) możemy obliczyć wartość czwartego wyrazu ciągu geometrycznego:
$$a_{n}=a_{1}\cdot q^{n-1} \\
a_{n}=a_{1}\cdot q^{n-1} \\
a_{4}=a_{1}\cdot 6^{4-1} \\
a_{4}=2\cdot6^3 \\
a_{4}=2\cdot216 \\
a_{4}=432$$ - Odpowiedź:
B. \(a_{4}=432\)
19. Wyznaczanie różnicy/ilorazu ciągu
Podpowiedź: W ciągach arytmetycznych sprawa jest prosta – dodatnia różnica oznacza, że ciąg jest rosnący. Jednak w ciągach geometrycznych nie jest to takie oczywiste i dodatni iloraz ciągu wcale nie musi dawać nam ciągu rosnącego. Przykładowo jak pierwszy wyraz jest równy \(-2\), to dodatni iloraz ciągu sprawia, że każdy kolejny wyraz robi się coraz mniejszy. Zawsze więc bądźmy ostrożni z wyciąganiem różnych wniosków.
Ostatnia deska ratunku: Jak szukamy wartości różnicy lub ilorazu, to możemy próbować podstawiać poszczególne odpowiedzi, sprawdzając która różnica lub który iloczyn będzie tym właściwym.
- Rozwiązanie:
Aby obliczyć różnicę tego ciągu wystarczy obliczyć różnicę między wartościami dwóch wyrazów sąsiednich.Krok 1. Obliczenie wartości ciągu dla \(n=1\) oraz \(n=2\).$$a_{1}=-2\cdot1+1=-2+1=-1 \\
a_{2}=-2\cdot2+1=-4+1=-3$$Krok 2. Obliczenie różnicy ciągu arytmetycznego.$$r=a_{2}-a_{1}=-3-(-1)=-2$$
Tak na marginesie, to wyliczona ujemna różnica \(r=-2\) świadczy o tym, że jest to ciąg malejący.
- Odpowiedź:
C. \(-2\)
- Rozwiązanie:
W tym zadaniu musimy obliczyć wartość ilorazu \(q\), a do tego celu wykorzystamy wzór na \(n\)-ty wyraz ciągu geometrycznego:
$$a_{n}=a_{1}\cdot q^{n-1}$$Korzystając z tego wzoru możemy podstawić podstawić nasze dane z zadania i otrzymamy:
$$a_{4}=a_{1}\cdot q^{4-1} \\
a_{4}=a_{1}\cdot q^{3} \\
\frac{a_{4}}{a_{1}}=q^{3} \\
q^{3}=\frac{24}{3} \\
q^{3}=8 \\
q=2$$ - Odpowiedź:
B. \(2\)
20. Obliczanie wartości wyrazu ciągu arytmetycznego/geometrycznego, gdy podane są trzy sąsiednie wyrazy
Podpowiedź: Dla trzech kolejnych wyrazów ciągu arytmetycznego zachodzi relacja: \(a_{2}=\frac{a_{1}+a_{3}}{2}\), natomiast dla trzech kolejnych wyrazów ciągu geometrycznego zachodzi relacja: \(a_{2}^2=a_{1}\cdot a_{3}\).
Ostatnia deska ratunku: Sprawdźmy zawsze, czy otrzymane wyniki mają w ogóle sens. Może się okazać, że jakieś rozwiązanie trzeba odrzucić chociażby dlatego, że ciąg jest rosnący.
- Rozwiązanie:
Skoro wskazane liczby są trzema kolejnymi wyrazami ciągu arytmetycznego, to zajdzie między nimi następująca równość:
$$a_{2}=\frac{a_{1}+a_{3}}{2}$$Podstawiając dane z treści zadania do powyższego wzoru wyznaczymy poszukiwaną wartość \(x\).
$$6=\frac{2x+1+16x+2}{2} \\
6=\frac{18x+3}{2} \\
12=18x+3 \\
18x=9 \\
x=\frac{1}{2}$$ - Odpowiedź:
\(x=\frac{1}{2}\)
- Rozwiązanie:
Skorzystamy tutaj ze wzoru na środkowy wyraz ciągu geometrycznego:
$${a_{n}}^2=a_{n-1}\cdot a_{n+1} \\
{a_{2}}^2=a_{2-1}\cdot a_{2+1} \\
{a_{2}}^2=a_{1}\cdot a_{3} \\
(2x+3)^2=x\cdot(4x+3) \\
4x^2+12x+9=4x^2+3x \\
9x+9=0 \\
9x=-9 \\
x=-1$$Skoro nasz pierwszy wyraz jest równy \(x\) to znaczy że jego wartość wynosi dokładnie \(-1\).
- Odpowiedź:
D. \(-1\)
21. Suma n początkowych wyrazów ciągu arytmetycznego/geometrycznego
Podpowiedź: Często problematycznym elementem tych zadań jest nieznajomość wartości pierwszego wyrazu. Jeżeli więc zajdzie taka konieczność, to trzeba wyznaczyć ten pierwszy wyraz czy to ze wzoru ciągu, czy też z informacji na temat innych znanych nam wyrazów i różnicy/iloczynu ciągu.
Ostatnia deska ratunku: Całej sumy wyrazów raczej ręcznie nie policzymy (no chyba, że tych wyrazów jest naprawdę mało), ale ręcznie możemy dochodzić do wartości pierwszego czy też ostatniego wyrazu, które trzeba podstawić do danego wzoru.
- Rozwiązanie:
Sumę \(n\)-początkowych wyrazów ciągu arytmetycznego możemy zapisać jako:
$$S_{n}=\frac{a_{1}+a_{n}}{2}\cdot n$$Naszym zadaniem jest tak naprawdę wyliczenie wartości dziesiątego wyrazu tego ciągu. Z treści zadania wiemy, że \(S_{n}=35\), oraz że \(a_{1}=3\), zatem bez problemu wyznaczymy poszukiwaną wartość \(a_{10}\):
$$35=\frac{3+a_{10}}{2}\cdot10 \\
35=(3+a_{10})\cdot5 \\
35=15+5a_{10} \\
20=5a_{10} \\
a_{10}=4$$ - Odpowiedź:
B. \(a_{10}=4\)
- Rozwiązanie:
Krok 1. Obliczenie wartości ilorazu \(q\).
Aby wyznaczyć wartość ilorazu \(q\) obliczmy sobie najpierw wartość pierwszego i drugiego wyrazu tego ciągu:
$$a_{n}=2n \\
a_{1}=2^1=2 \\
a_{2}=2^2=4$$$$q=\frac{a_{2}}{a_{1}}=\frac{4}{2}=2$$
Krok 2. Obliczenie sumy dziesięciu pierwszych wyrazów.Znając wartość ilorazu \(q\) oraz wartość pierwszego wyrazu, możemy skorzystać z następującego wzoru:
$$S_{n}=a_{1}\cdot\frac{1-q^n}{1-q} \\
S_{10}=2\cdot\frac{1-2^{10}}{1-2} \\
S_{10}=2\cdot\frac{1-2^{10}}{-1} \\
S_{10}=-2\cdot(1-2^{10})$$ - Odpowiedź:
B. \(-2(1-2^{10})\)
22. Odczytywanie wartości funkcji trygonometrycznych z tablic
Podpowiedź: Kąty dla sinusów i tangensów odczytujemy z kolumny \(α\), natomiast kąty dla cosinusów odczytujemy z kolumny \(β\).
Ostatnia deska ratunku: Zazwyczaj interesują nas kąty \(30°\), \(45°\) lub \(60°\), a wartości tych kątów znajdziemy w małej tabelce trygonometrycznej (jest w tablicach w dziale „trygonometria”).
- Rozwiązanie:
W tym zadaniu tak naprawdę musimy tylko odczytać z tablic poszczególne wartości i wykonać poprawnie działania na pierwiastkach i potęgach:
$$(tg60°+tg45°)^2-sin60°= \\
=(\sqrt{3}+1)^2-\frac{\sqrt{3}}{2}= \\
=3+2\sqrt{3}+1-\frac{\sqrt{3}}{2}= \\
=\frac{2\cdot(3+2\sqrt{3}+1)}{2}-\frac{\sqrt{3}}{2}= \\
=\frac{8+4\sqrt{3}}{2}-\frac{\sqrt{3}}{2}= \\
=-\frac{8+3\sqrt{3}}{2}= \\
=4+\frac{3\sqrt{3}}{2}$$ - Odpowiedź:
D. \(4+\frac{3\sqrt{3}}{2}\)
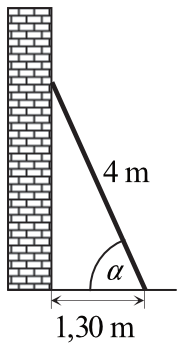
Kąt \(α\), pod jakim ustawiono drabinę, spełnia warunek:
- Rozwiązanie:
Krok 1. Wyznaczenie wartości \(cosα\).
Z funkcji trygonometrycznych w trójkącie prostokątnym wynika, że zależność między przyprostokątną leżącą przy danym kącie, a przeciwprostokątną możemy opisać funkcją cosinus:
$$cosα=\frac{1,30}{4} \\
cosα=0,325$$Krok 2. Odczytanie miary kąta z tablic trygonometrycznych.Musimy teraz poprawnie odczytać z tablic trygonometrycznych dla jakiego kąta ostrego funkcja cosinus przyjmuje wartość około \(0,325\). Najbliżej tej wartości jest kąt \(71°\), zatem \(60°\lt α\lt 90°\).
Uwaga! Wiele osób błędnie odczytuje z tablic, że poszukiwanym kątem jest ten o mierze \(19°\). To byłby kąt \(19°\) gdybyśmy mieli funkcję sinus, a nie cosinus.
- Odpowiedź:
D. \(60°\lt α\lt 90°\)
23. Mając wartość jednej funkcji trygonometrycznej, wyznacz wartość innej funkcji
Podpowiedź: W takich zadaniach trzeba zazwyczaj korzystać z jedynki trygonometrycznej i z tego, że \(tgα=\frac{sinα}{cosα}\).
Ostatnia deska ratunku: Tak prawdę mówiąc to jak podadzą nam że np. \(sinα=\frac{3}{5}\) i szukamy wartości cosinusa czy tangensa dla tego kąta, to możemy w tablicach sprawdzić dla jakiego kąta \(α\) sinus przyjmuje wartość równą \(\frac{3}{5}\) (w przybliżeniu oczywiście). Jak już znamy miarę kąta \(α\), to możemy sprawdzić jaką wartość przyjmuje ten cosinus/tangens dla tego kąta. Wyniki wyjdą nam w pewnym przybliżeniu, ale zazwyczaj przybliżenie będzie na tyle dobre, że bez problemu wskażemy poprawną odpowiedź.
- Rozwiązanie:
Skorzystamy tutaj z tzw. „jedynki trygonometrycznej”, podstawiając do wzoru wartość cosinusa:
$$sin^2α+cos^2α=1 \\
sin^2α+\left(\frac{3}{4}\right)^2=1 \\
sin^2α+\frac{9}{16}=1 \\
sin^2α=\frac{7}{16} \\
sinα=\sqrt{\frac{7}{16}} \quad\lor\quad sinα=-\sqrt{\frac{7}{16}} \\
sinα=\frac{\sqrt{7}}{4} \quad\lor\quad sinα=-\frac{\sqrt{7}}{4}$$Z racji tego iż kąt \(α\) jest ostry, to sinus musi przyjąć wartość dodatnią, stąd też prawidłowa jest odpowiedź \(sinα=\frac{\sqrt{7}}{4}\).
- Odpowiedź:
C. \(\frac{\sqrt{7}}{4}\)
- Rozwiązanie:
Krok 1. Obliczenie wartości cosα.
Z jedynki trygonometrycznej wiemy, że \(sin^2α+cos^2α=1\), zatem:
$$cos^2α=1-sin^2α \\
cos^2α=1-\left(\frac{7}{13}\right)^2 \\
cos^2α=1-\frac{49}{169} \\
cos^2α=\frac{120}{169} \\
cosα=\sqrt{\frac{120}{169}} \quad\lor\quad cosα=-\sqrt{\frac{120}{169}} \\
cosα=\frac{\sqrt{120}}{13} \quad\lor\quad cosα=-\frac{\sqrt{120}}{13}$$Kąt \(α\) jest ostry, więc ujemną wartość cosinusa odrzucamy.
Krok 2. Obliczenie wartości \(tgα\).Znając wartość sinusa i cosinusa bez problemu wyliczymy wartość tangensa:
$$tgα=\frac{sinα}{cosα} \\
tgα=\frac{\frac{7}{13}}{\frac{\sqrt{120}}{13}} \\
tgα=\frac{7}{13}:\frac{\sqrt{120}}{13} \\
tgα=\frac{7}{13}\cdot\frac{13}{\sqrt{120}} \\
tgα=\frac{7}{\sqrt{120}}$$ - Odpowiedź:
C. \(\frac{7}{\sqrt{120}}\)
24. Obliczanie wartości funkcji trygonometrycznych dla kątów rozwartych
Podpowiedź: Aby obliczyć wartość funkcji trygonometrycznej dla kątów rozwartych musimy skorzystać ze wzorów redukcyjnych. Znajdziesz je tutaj: Wzory redukcyjne
Ostatnia deska ratunku: W tablicach maturalnych znajdują się wykresy funkcji trygonometrycznych. Na upartego możemy odczytać z nich przybliżoną wartość interesującego nas kąta rozwartego. Musimy tylko wiedzieć, że \(\frac{\pi}{2}\) to \(90°\), a \(\pi\) to \(180°\).
- Rozwiązanie:
Musimy skorzystać z jednego ze wzorów redukcyjnych:
$$sin(90°+α)=cosα \\
sin150°=sin(90°+60°)=cos60°$$ - Odpowiedź:
A. \(cos60°\)
- Rozwiązanie:
To zadanie jest bardzo proste do policzenia, o ile pamiętamy że w tablicach matematycznych znajduje się następujący wzór:
$$P=a^2\cdot sinα$$Zanim jednak skorzystamy z tego wzoru to musimy jeszcze wyznaczyć wartość sinusa \(150°\).
Krok 1. Obliczenie wartości \(sin150°\).W tablicach trygonometrycznych nie znajdziemy wartości sinusa dla kątów rozwartych. Musimy więc skorzystać z tzw. wzorów redukcyjnych:
$$sin(180-α)=sinα \\
sin(180°-30°)=sin30° \\
sin150°=sin30°$$To oznacza, że \(sin150°\) będzie równy \(sin30°\), czyli \(\frac{1}{2}\).
Krok 2. Obliczenie pola powierzchni rombu.$$P=a^2\cdot sinα \\
P=6^2\cdot sin150° \\
P=36\cdot\frac{1}{2} \\
P=18$$ - Odpowiedź:
B. \(18\)
25. Kąt środkowy i wpisany
Podpowiedź: Kluczem do sukcesu jest tutaj oczywiście pamiętanie o tym, że jeżeli kąt środkowy jest opisany na tym samym łuku co kąt wpisany, to miara tego kąta środkowego będzie dwukrotnie większa od kąta wpisanego. Cała trudność tych zadań polega zazwyczaj na tym, by dobrze sprawdzać na jakich łukach są opisane poszczególne kąty. Warto też dodać tutaj informację, że jeżeli okrąg jest podzielony np. na \(6\) równych części, to miara kąta środkowego oparta na takim pojedynczym fragmencie łuku będzie równa \(\frac{1}{6}\cdot360=60°\).
Ostatnia deska ratunku: Rysunki na maturze są zazwyczaj dokładne, a to oznacza że możemy oszacować jaką miarę ma kąt na naszym rysunku, zwłaszcza gdy proponowane odpowiedzi są dosyć zróżnicowane. No dobrze, ale jak określić miary kąta na rysunku, skoro nie mamy kątomierza. Fakt, kątomierza nie mamy, ale parę miar kątów jesteśmy w stanie „wygenerować”. Tak przykładowo, to jak narysujesz sobie trójkąt prostokątny o przyprostokątnych \(3\) i \(3\), to otrzymasz kąty \(45°\). Jak narysujesz trójkąt prostokątny o bokach \(3,4,5\), to ten mniejszy kąt ostry ma miarę około \(37°\), a większy ma \(53°\). Jak narysujesz sobie trójkąt równoboczny, to otrzymasz kąt \(60°\) i tak dalej. Można więc w ten sposób dość dobrze porównać miary kątów z tym co jest na głównym rysunku.
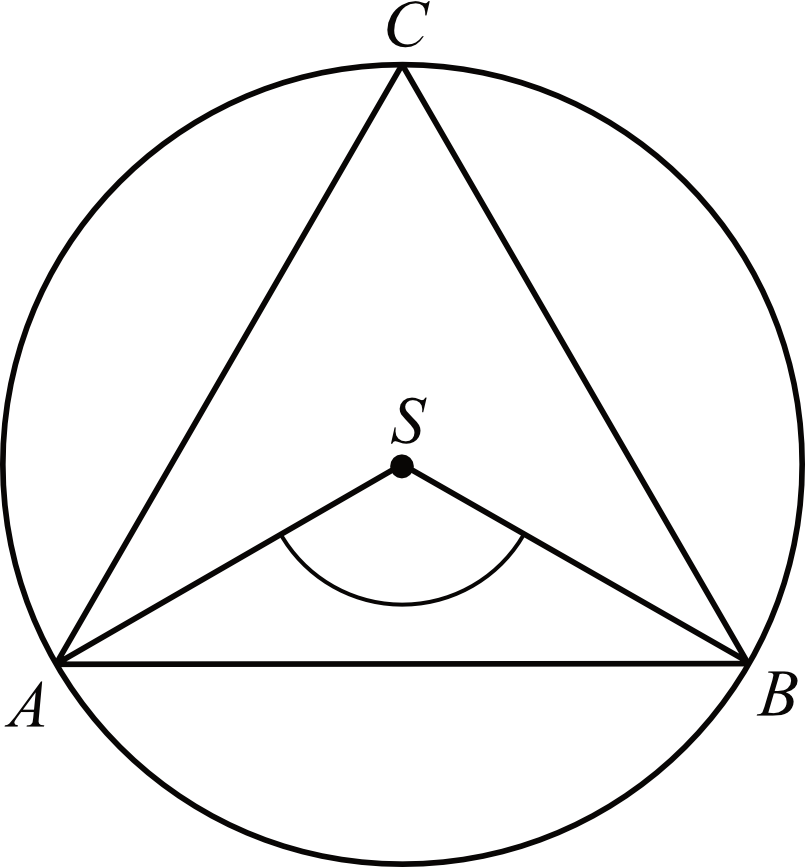
- Rozwiązanie:
Chcąc obliczyć to zadanie wystarczy skorzystać z własności kątów środkowych i wpisanych, pamiętając o tym, że każdy kąt w trójkącie równobocznym ma miarę \(60°\). Widzimy, że kąty \(ACB\) oraz \(ASB\) są oparte na tym samym łuku. Skoro kąt \(ACB\) wpisany na okręgu ma \(60°\), to kąt środkowy \(ASB\) ma \(2\cdot60°\), czyli \(120°\).Tak na marginesie – to zadanie dałoby się praktycznie rozwiązać bez obliczeń, bo już z samego rysunku widać, że zaznaczony kąt jest kątem rozwartym, a tylko \(120°\) jest takim kątem.
- Odpowiedź:
A. \(120°\)
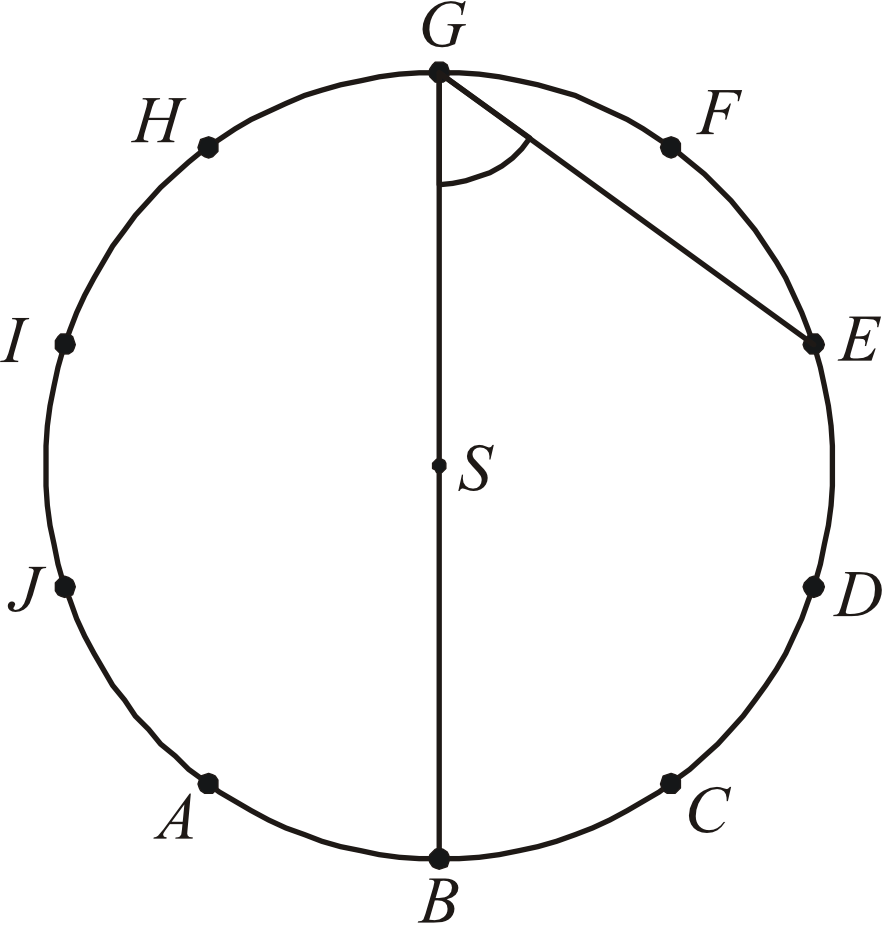
- Rozwiązanie:
Krok 1. Obliczenie miary kąta \(BSE\).
Dorysujmy sobie odcinek \(SE\) i obliczmy miarę kąta środkowego \(BSE\).
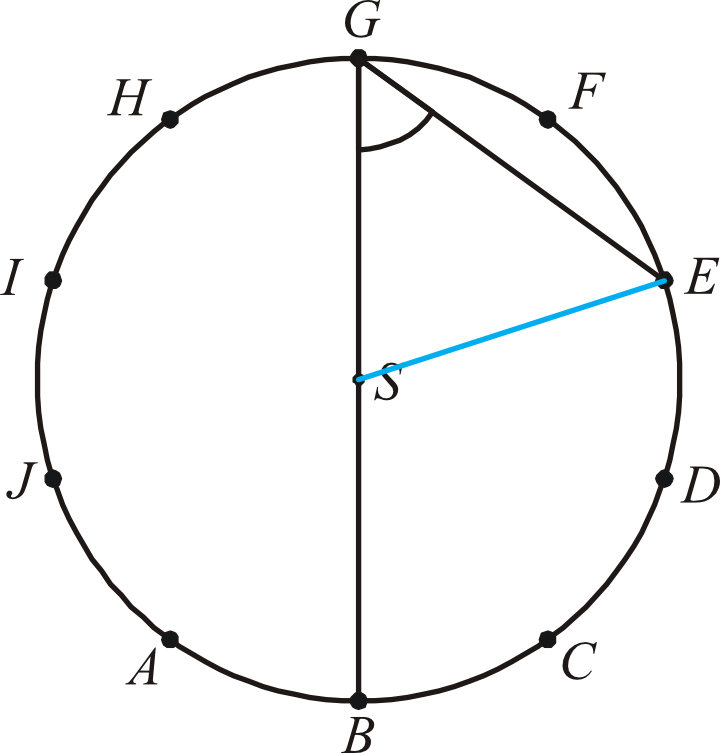
Widzimy, że kąt ten stanowi trzy z dziesięciu „cząstek” kąta pełnego, zatem jego miara jest równa:
$$|\sphericalangle BSE|=\frac{3}{10}\cdot360° \\
|\sphericalangle BSE|=108°$$Krok 2. Obliczenie miary kąta \(BGE\).Kąt \(BGE\) jest oparty na tym samym łuku co kąt środkowy \(BSE\), którego miarę obliczyliśmy przed chwilą. W związku z tym zgodnie z własnościami kątów wpisanych i środkowych kąt ten będzie dwa razy mniejszy od kąta \(BSE\):
$$|\sphericalangle BGE|=108°:2 \\
|\sphericalangle BGE|=54°$$ - Odpowiedź:
A. \(54°\)
26. Styczna do okręgu i okręgi styczne
Podpowiedź: Styczna do okręgu tworzy z promieniem okręgu zawsze kąt prosty i jest to własność z której bardzo często w tym temacie korzystamy.
Ostatnia deska ratunku: W zadaniach ze stycznymi często będzie pojawiał się trójkąt równoramienny, gdzie ramionami są promienie okręgu.
- Rozwiązanie:
Kluczem do sukcesu w tym zadaniu jest sporządzenie poprawnego rysunku szkicowego.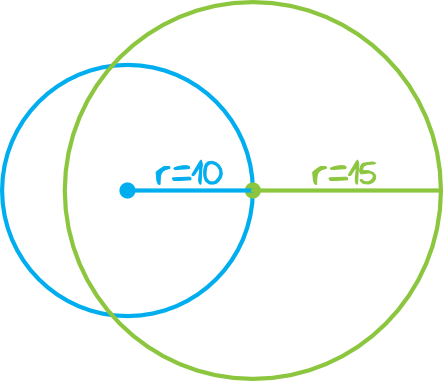
Szukamy długości między środkami tych okręgów. Z rysunku wynika, że ta odległość jest równa \(10\) i taka też jest nasza odpowiedź na to zadanie.
- Odpowiedź:
C. \(10\)
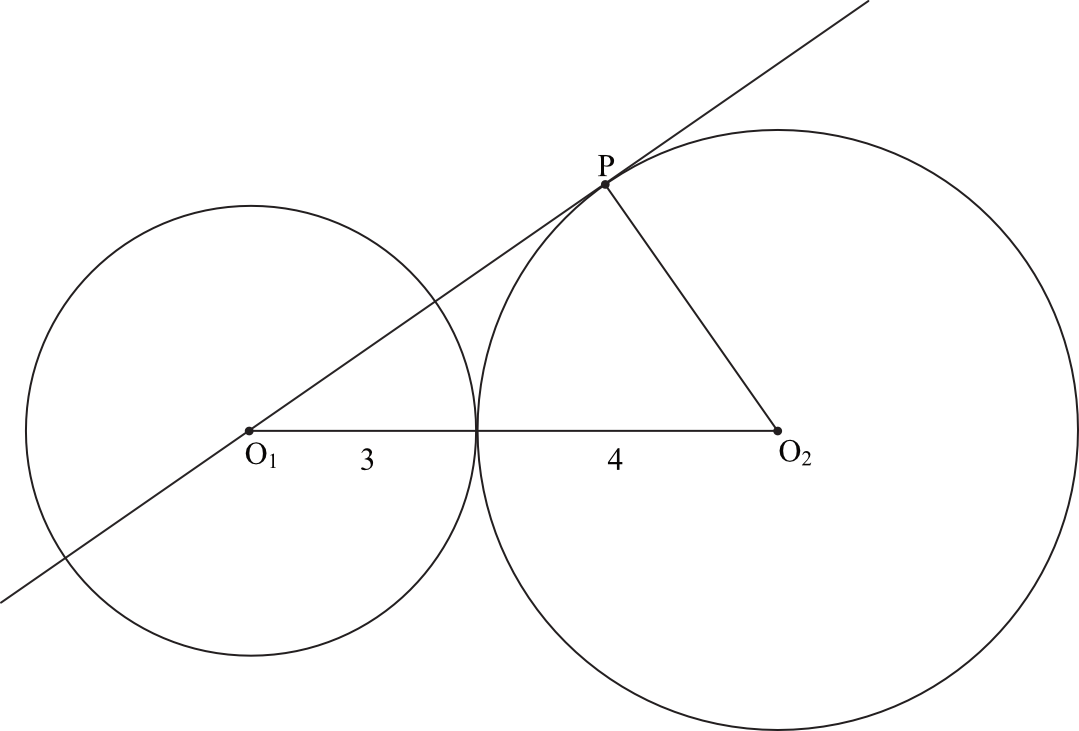
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe:
- Rozwiązanie:
Krok 1. Obliczenie długości odcinka \(PO_{1}\).
Musimy dostrzec, że powstały trójkąt jest prostokątny. Skoro tak, to będziemy mogli skorzystać w nim z Twierdzenia Pitagorasa. Musimy też zauważyć, że odcinek \(PO_{2}\) ma długość równą \(4\), bo jest to po prostu promień naszego okręgu. Skoro tak, to możemy teraz wyznaczyć długość przyprostokątnej \(PO_{1}\):
$$a^2+b^2=c^2 \\
|PO_{2}|^2+|PO_{1}|^2=|O_{1}O_{2}|^2 \\
4^2+|PO_{1}|^2=7^2 \\
16+|PO_{1}|^2=49 \\
|PO_{1}|^2=33 \\
|PO_{1}|=\sqrt{33}$$Krok 2. Obliczenie pola powierzchni.Obliczona przez nas długość odcinka \(|PO_{1}|=\sqrt{33}\) jest jednocześnie wysokością naszego trójkąta prostokątnego o podstawie \(|PO_{2}|=4\). Pole powierzchni tej figury jest więc równe:
$$P=\frac{1}{2}\cdot|PO_{2}|\cdot|PO_{1}| \\
P=\frac{1}{2}\cdot4\cdot\sqrt{33} \\
P=2\sqrt{33}$$ - Odpowiedź:
B. \(2\sqrt{33}\)
27. Trójkąty podobne lub przystające
Podpowiedź: Pamiętaj, że trójkąty podobne to trójkąty mające identyczne miary kątów, ale różne długości boków (jeden trójkąt jest wtedy większy od drugiego). Trójkąty przystające mają jednakowe miary kątów i jednakowe miary boków (czyli są one identyczne i wcale nie muszą się ze sobą stykać). Często też będzie tak, że trójkąty podobne będą narysowane tak jakby „jeden w drugim”.
Ostatnia deska ratunku: W kryzysowych sytuacjach może nam pomóc po prostu linijka. Możemy sobie zmierzyć jaką długość ma na rysunku poszukiwany przez nas bok i sprawdzić jak ma się ta miara do pozostałych boków. Dzięki temu będziemy w stanie podać dobrą długość poszukiwanego boku. Może też zdarzyć się i taka sytuacja, że w zadaniu dowodowym trzeba będzie coś udowodnić wykorzystując trójkąty podobne i nie będziemy pewni czy rzeczywiście są one podobne, czy nie. Nic więc nie stoi na przeszkodzie sprawdzić sobie wstępnie linijką stosunki poszczególnych boków, a jak się upewnimy że trójkąty są lub nie są podobne, to będziemy mogli kombinować dalej.
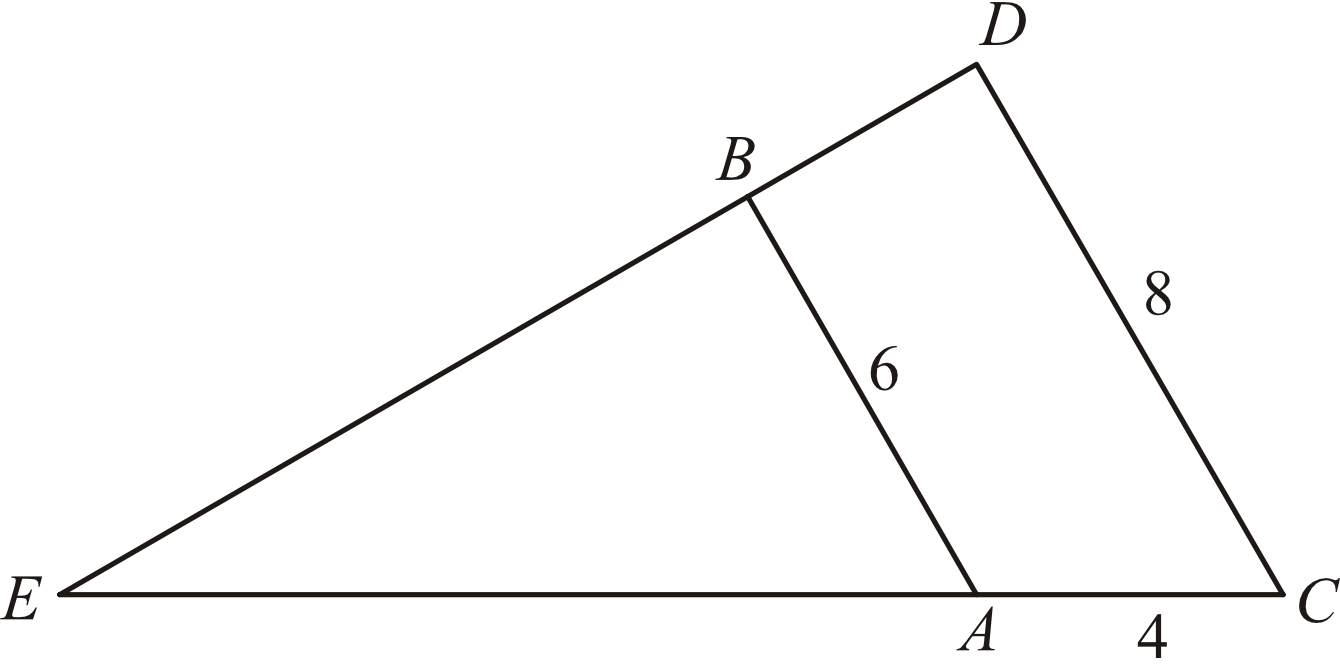
- Rozwiązanie:
Krok 1. Zbudowanie równania na podstawie danych z treści zadania.
Wiedząc, że proste \(AB\) oraz \(CD\) są równoległe możemy stwierdzić, że trójkąty \(EAB\) oraz \(ECD\) są trójkątami podobnymi. W związku z tym prawdziwa będzie relacja:
$$\frac{|EA|}{|AB|}=\frac{|EC|}{|CD|} \\
\frac{x}{6}=\frac{x+4}{8}$$Zwróć szczególną uwagę na odcinek \(EC\). Bardzo często w tego typu zadaniach uczniowie wpisują w tym miejscu długość odcinka \(AC\), co jest błędem.
Krok 2. Rozwiązanie powstałego równania.Najprościej będzie wykonać mnożenie na krzyż, zatem:
$$8x=6\cdot(x+4) \\
8x=6x+24 \\
2x=24 \\
x=12$$Długość odcinka \(|AE|\) oznaczono na rysunku jako \(x\), więc \(|AE|=12\).
- Odpowiedź:
D. \(|AE|=12\)
- Rozwiązanie:
Musimy obliczyć skalę podobieństwa boku \(A’B’\) względem \(AB\). Matematycznie rzecz ujmując skalę podobieństwa zapiszemy jako \(\frac{A’B’}{AB}=k\). Naszym zadaniem jest teraz wyznaczyć wartość tego współczynnika \(k\) korzystając z wiedzy na temat pól trójkątów podanych w treści zadania. Jeżeli dwie figury są figurami podobnymi, to ich pola są do siebie podobne w skali \(k^2\). To pozwoli nam ułożyć następujące równanie:
$$k^2=\frac{P_{A’B’C’}}{P_{ABC}} \\
k^2=\frac{50cm^2}{25cm^2} \\
k^2=2 \\
k=\sqrt{2}$$W ten sposób korzystając z pól powierzchni obliczyliśmy skalę podobieństwa \(k\) między dwoma bokami trójkąta, czyli dokładnie to czego szukaliśmy w tym zadaniu.
- Odpowiedź:
C. \(\sqrt{2}\)
28. Równanie prostej przechodzącej przed dwa punkty
Podpowiedź: Równanie prostej możemy wyznaczyć albo korzystając z układu równań (wtedy pod postać \(y=ax+b\) podstawiamy współrzędne raz jednego, raz drugiego punktu), albo korzystając ze wzoru dostępnego w tablicach \((y-y_{A})(x_{B}-x_{A})-(y_{B}-y_{A})(x-x_{A})=0\).
Ostatnia deska ratunku: W bardzo rozbudowanych zadaniach często musimy wyznaczyć równanie jakiejś prostej tylko po to, by móc uzyskać z niej współczynnik kierunkowy \(a\), który jest potrzebny do wyznaczenia prostej prostopadłej lub równoległej. No i właśnie, jak już kompletnie nie potrafimy napisać wzoru takiej prostej (albo coś nam nie po prostu wychodzi) to możemy chociaż spróbować wyznaczyć współczynnik kierunkowy \(a\). Jest to dość łatwe, bo możemy skorzystać ze wzoru: \(a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}\). Może się okazać, że wyznaczając ten współczynnik \(a\) zdobędziemy dodatkowe punkty, a i kto wie czy nie popchnie nas to dalej do rozwiązania kolejnych kroków zadania.
- Rozwiązanie:
Prostą przechodzącą przez dwa punkty \(M=(x_{M};y_{M})\) oraz \(N=(x_{N};y_{N})\) możemy opisać następującym równaniem:
$$(y-y_{M})(x_{N}-x_{M})-(y_{N}-y_{M})(x-x_{M})=0 \\
(y-(-5))(-1-3)-(7-(-5))(x-3)=0 \\
(y+5)\cdot(-4)-12\cdot(x-3)=0 \\
-4y-20-12x+36=0 \\
-4y-12x+16=0 \\
-4y=12x-16 \quad\bigg/:(-4) \\
y=-3x+4$$ - Odpowiedź:
A. \(y=-3x+4\)
- Rozwiązanie:
Współczynnik kierunkowy prostej przechodzącej przed dwa punkty \(A=(x_{1};y_{1})\) oraz \(B=(x_{2};y_{2})\) wyraża się wzorem:
$$a=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$Mamy wszystkie dane, więc wystarczy podstawić odpowiednie liczby i w ten sposób obliczymy współczynnik \(a\):
$$a=\frac{3-1}{3-6}=\frac{2}{-3}=-\frac{2}{3}$$ - Odpowiedź:
A. \(-\frac{2}{3}\)
29. Długość odcinka
Podpowiedź: Umiejętność obliczania długości odcinka przydaje się nie tylko w prostych zadaniach zamkniętych, ale także w zadaniach gdzie mamy jakieś figury geometryczne narysowane w układzie współrzędnych. Może być właśnie tak, że znając jakieś współrzędne wierzchołków figury będziemy w stanie wyznaczyć jakąś długość boku.
Ostatnia deska ratunku: Jak mamy dobry rysunek pomocniczy to możemy linijką sprawdzić czy obliczona długość jest rzeczywiście poprawna.
- Rozwiązanie:
Skorzystamy ze wzoru na długość odcinka w układzie współrzędnych, czyli tak naprawdę na odległość między dwoma punktami:
$$|PQ|=\sqrt{(x_{Q}-x_{P})^2+(y_{Q}-y_{P})^2} \\
|PQ|=\sqrt{(3-(-2))^2+(3-(-2))^2} \\
|PQ|=\sqrt{5^2+5^2} \\
|PQ|=\sqrt{25+25} \\
|PQ|=\sqrt{25\cdot2} \\
|PQ|=5\sqrt{2}$$ - Odpowiedź:
C. \(5\sqrt{2}\)
- Rozwiązanie:
Krok 1. Obliczenie długości boku rombu.
Z treści zadania możemy wyczytać, że punkty \(A\) i \(B\) są kolejnymi wierzchołkami rombu, czyli że tworzoną one odcinek, który jest jednocześnie bokiem naszej figury. Na początku więc obliczmy długość tego odcinka. Skorzystamy tutaj ze wzoru na długość odcinka, znając jego współrzędne:
$$a=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$$\(x_{1}\) oraz \(y_{1}\) to współrzędne pierwszego punktu, a \(x_{2}\) oraz \(y_{2}\) to współrzędne drugiego punktu.
Podstawiając współrzędne \(A=(-1;2)\) i \(B=(5;-2)\) otrzymamy:
$$a=\sqrt{(5-(-1))^2+(-2-2)^2} \\
a=\sqrt{6^2+(-4)^2} \\
a=\sqrt{36+16} \\
a=\sqrt{52} \\
a=\sqrt{4\cdot13} \\
a=2\sqrt{13}$$Krok 2. Obliczenie obwodu rombu.Znamy długość jednego z boków rombu, a wiemy że romb ma cztery boki równej długości. To znaczy, że:
$$Obw=4a \\
Obw=4\cdot2\sqrt{13} \\
Obw=8\sqrt{13}$$ - Odpowiedź:
D. \(8\sqrt{13}\)
30. Środek odcinka
Podpowiedź: Pamiętaj, że przekątne kwadratu, prostokąta lub rombu przecinają się w połowie swojej długości, czyli tutaj także możemy czasem skorzystać z własności środka odcinka.
Ostatnia deska ratunku: Często dobrą praktyką jest oddzielne obliczanie współrzędnej iksowej i oddzielne współrzędnej igrekowej. Możemy zapisać więc, że \(x_{S}=\frac{x_{A}+x_{B}}{2}\) oraz \(y_{S}=\frac{y_{A}+y_{B}}{2}\).
- Rozwiązanie:
Współrzędne środka odcinka \(S=(x_{S};y_{S})\) wyznaczymy ze wzoru:
$$S=(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2})$$Znając współrzędne środka oraz jednego z punktów, możemy wykorzystać ten wzór do wyznaczenia współrzędnych punktu \(B\). Oczywiście można też podstawiać po kolei współrzędne ze wszystkich odpowiedzi, ale spróbujmy to zadanie rozwiązać tak, jakby było ono zadaniem otwartym.
Krok 1. Obliczenie współrzędnej \(x_{B}\).$$x_{S}=\frac{x_{A}+x_{B}}{2} \\
2=\frac{-1+x_{B}}{2} \\
4=-1+x_{B} \\
x_{B}=5$$Tak naprawdę już w tym momencie możemy zakończyć obliczenia, bo już widzimy, że pasującą odpowiedzią może być tylko \(A\). Obliczmy jeszcze jednak współrzędną \(y_{B}\).
Krok 2. Obliczenie współrzędnej \(y_{B}\).$$y_{S}=\frac{y_{A}+y_{B}}{2} \\
7=\frac{3+y_{B}}{2} \\
14=3+y_{B} \\
y_{B}=11$$To oznacza, że poszukiwanymi współrzędnymi są \(B=(5,11)\).
- Odpowiedź:
A. \(B=(5,11)\)
- Rozwiązanie:
Skorzystamy tutaj ze wzoru na wyznaczenie współrzędnych środka odcinka:
$$M=(x_{M};y_{M})=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right)$$Naszym zadaniem jest tak naprawdę wyliczenie z tego wzoru wartości \(x_{A}\) (bo jest ona opisana niewiadomą \(a\)) oraz wartości \(y_{B}\) (która jest opisana niewiadomą \(b\)).
Krok 1. Obliczenie wartości niewiadomej \(a\).$$x_{M}=\frac{x_{A}+x_{B}}{2} \\
3=\frac{a+7}{2} \\
6=a+7 \\
a=-1$$Krok 2. Obliczenie wartości niewiadomej \(b\).$$y_{M}=\frac{y_{A}+y_{B}}{2} \\
4=\frac{6+b}{2} \\
8=6+b \\
b=2$$ - Odpowiedź:
B. \(a=-1\) i \(b=2\)
31. Proste prostopadłe lub równoległe
Podpowiedź: Proste są równoległe, gdy mają identyczne współczynniki kierunkowe \(a\), natomiast prostopadłe są wtedy, gdy iloczyn współczynników kierunkowych \(a\) jednej i drugiej prostej jest równy \(-1\).
Ostatnia deska ratunku: Jeżeli szukamy wzoru prostej prostopadłej lub równoległej, to bardzo pomocny może być rysunek szkicowy. Warto wtedy po kratkach narysować sobie to co wiemy z treści zadania i dorysować do tego wszystkiego poszukiwaną prostą prostopadłą lub równoległą. Często pozwoli nam to dostrzec jakąś kluczową informację (np. jakiś ważny punkt przecięcia się wykresu z osią iksów lub igreków).
- Rozwiązanie:
Krok 1. Ustalenie wartości współczynnika \(a\).
Aby dwie proste w postaci \(y=ax+b\) były względem siebie prostopadłe to iloczyn ich współczynników kierunkowych \(a\) musi być równy \(-1\). Nasza pierwsza prosta ma współczynnik \(a=-\frac{1}{3}\), zatem współczynnik kierunkowy prostej prostopadłej jest równy:
$$-\frac{1}{3}\cdot a=-1 \\
a=3$$Krok 2. Ustalenie wartości współczynnika \(b\).Współczynnik \(b\) mówi nam o tym w którym miejscu wykres prostej przetnie się z osią \(Oy\). Skoro prosta ma przechodzić przez początek układu współrzędnych, czyli punkt o współrzędnych \((0;0)\), to oznacza, że \(b=0\).
Równanie poszukiwanej prostej prostopadłej to w takim razie: \(y=3x\).
- Odpowiedź:
A. \(y=3x\)
- Rozwiązanie:
Krok 1. Ustalenie wartości współczynnika kierunkowego \(a\).
Aby dwie proste w postaci \(y=ax+b\) były względem siebie równoległe to warunkiem koniecznym jest to, aby miały one identyczny współczynnik kierunkowy \(a\). W naszym przykładzie prosta \(k\) ma współczynnik \(a=2\), więc prosta \(l\) musi mieć dokładnie taki sam współczynnik kierunkowy, dlatego będzie ona na pewno opisana wzorem \(y=2x+b\). Dzięki temu już na \(100\%\) wiemy, że pod uwagę bierzemy już tylko drugą i trzecią odpowiedź.
Krok 2. Ustalenie wartości współczynnika \(b\).Teraz musimy ustalić jaka jest brakująca wartość współczynnika \(b\). Do wzoru \(y=2x+b\) podstawimy współrzędne naszego punktu \(D=(-2,1)\), czyli \(x=-2\) oraz \(y=1\), dzięki czemu poznamy wartość współczynnika \(b\).
$$y=2x+b \\
1=2\cdot(-2)+b \\
1=-4+b \\
b=5$$Krok 3. Zapisanie wzoru poszukiwanej prostej.Skoro \(a=2\) oraz \(b=5\), to prosta \(l\) ma postać \(y=2x+5\).
- Odpowiedź:
C. \(y=2x+5\)
32. Równanie z parametrem
Podpowiedź: Zazwyczaj równanie z parametrem będzie miało coś wspólnego ze wzorem prostej/funkcji i wtedy ten parametr będzie ukryty w jakimś konkretnym współczynniku (np. może być ukryty we współczynniku \(a\) funkcji liniowej). W takiej sytuacji musimy pamiętać za co odpowiedzialny jest konkretny współczynnik i jaka powinna być docelowo jego wartość. Jeżeli mamy prostą np. \(y=(m+3)x-6\) i wiemy, że prosta jest rosnąca, to musimy sprawdzić kiedy ta nasza wartość \(m+3\) jest większa od zera, bo dla prostych rosnących współczynnik \(a\) jest przecież dodatni.
Ostatnia deska ratunku: Zdarza się, że zadanie z parametrem da się rozwiązać podstawiając po prostu po kolei proponowane odpowiedzi.
- Rozwiązanie:
Aby dwie proste były względem siebie równoległe to muszą mieć jednakowy współczynnik kierunkowy \(a\). Pierwsza prosta ma współczynnik kierunkowy \(a=m\). Druga ma \(a=1-2m\), zatem:
$$m=1-2m \\
3m=1 \\
m=\frac{1}{3}$$ - Odpowiedź:
C. \(m=\frac{1}{3}\)
- Rozwiązanie:
Skoro punkt \(S=(5,-2)\) należy do funkcji, to możemy podstawić jego współrzędne do wzoru funkcji i w ten sposób wyliczyć parametr \(m\).
$$-2=(m-1)\cdot5+3 \\
-2=5m-5+3 \\
-2=5m-2 \\
5m=0 \\
m=0$$ - Odpowiedź:
B. \(m=0\)
33. Zadania z figurami płaskimi
Podpowiedź: Tu zadania mogą być różnorodne, same figury mogą też przydać się w dużym zadaniu otwartym z bryłami. Z takich kluczowych rzeczy o których czasem zapominacie to własności figur płaskich. Podam więc może trzy takie najistotniejsze, które często Wam umykają. Po pierwsze – w trójkącie równoramiennym kąty przy podstawie mają jednakową miarę. Po drugie – wysokość pada zawsze na podstawę pod kątem prostym (czyli co za tym idzie – powstaje nam gdzieś trójkąt prostokątny, zatem często będziemy skorzystać tam z Twierdzenia Pitagorasa czy też z funkcji trygonometrycznych). Po trzecie – w tablicach matematycznych mamy parę ciekawych wzorów na pola powierzchni figur, które to wzory wykorzystują funkcje trygonometryczne. Jak w zadaniu jest podany kąt i zadanie jest związane w jakiś sposób z polem powierzchni, to często te wzory błyskawicznie zaprowadzą nas do sukcesu.
Ostatnia deska ratunku: Jeżeli zadanie jest zamknięte, a nam brakuje długości jakiegoś boku lub jakiejś wysokości (np. do policzenia pola powierzchni), to może się okazać, że tę brakującą wartość odczytamy z pomocą linijki (przynajmniej w przybliżeniu).
- Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
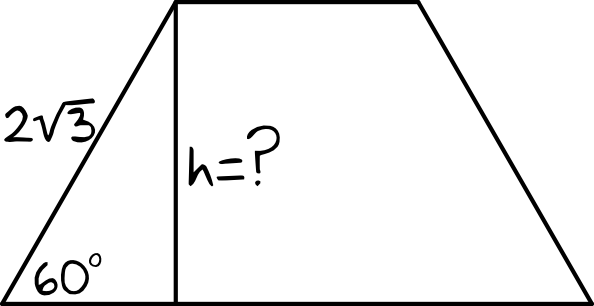
Z rysunku widać wyraźnie, że wartość \(h\) (czyli wysokość naszego trapezu) wyliczymy korzystając z sinusa kąta \(60°\). Możemy też zastosować tutaj własności trójkątów o kątach \(30°, 60°, 90°\).
Krok 2. Obliczenie wysokości trapezu.$$sin60°=\frac{h}{2\sqrt{3}} \\
\frac{\sqrt{3}}{2}=\frac{h}{2\sqrt{3}} \\
h=\frac{\sqrt{3}}{2}\cdot2\sqrt{3} \\
h=\sqrt{3}\cdot\sqrt{3}=3$$ - Odpowiedź:
B. \(3\)
- Rozwiązanie:
Krok 1. Obliczenie długości boku rombu.
Znając miarę kąta między bokami rombu oraz jego pole powierzchni, możemy wyznaczyć długość boku rombu z następującego wzoru dostępnego w tablicach matematycznych:
$$P=a^2\cdot sinα \\
50\sqrt{2}=a^2\cdot sin45° \\
50\sqrt{2}=a^2\cdot\frac{\sqrt{2}}{2} \quad\bigg/\cdot2 \\
100\sqrt{2}=a^2\cdot\sqrt{2} \quad\bigg/:\sqrt{2} \\
a^2=100 \\
a=10$$Krok 2. Obliczenie wysokości rombu.Znamy pole powierzchni, znamy długość boku rombu, więc do wyznaczenia poszukiwanej wysokości możemy posłużyć się następującym wzorem na pole rombu:
$$P=a\cdot h \\
50\sqrt{2}=10\cdot h \\
h=5\sqrt{2}$$ - Odpowiedź:
\(h=5\sqrt{2}\)
34. Zadania z graniastosłupem/ostrosłupem.
Podpowiedź: Jeżeli graniastosłup/ostrosłup jest prawidłowy, to znaczy że w podstawie ma figurę foremną czyli np. trójkąt równoboczny, kwadrat itd. Może się więc okazać, że korzystając z własności takiej figury, uda nam się wyznaczyć brakującą długość do obliczenia objętości lub pola powierzchni całkowitej.
Ostatnia deska ratunku: Takie zadania zazwyczaj są w części otwartej, sprawdzany więc będzie sposób rozwiązania zadania. Jednak bardzo często punkt można nie tylko za obliczenia, ale za sam rysunek. Spróbuj więc na rysunku zaznaczyć to co jest podane w treści zadania, to czego szukamy oraz jakieś kluczowe rzeczy które widzisz że mogą się przydać (np. wysokość ostrosłupa, może jakaś przekątna kwadratu w podstawie itd.). Nie bój się też wyliczać różne długości, często nawet za obliczenie przekątnej kwadratu znajdującego się w podstawie można dostać punkt, bo potem się okazuje że był to jeden z kroków na drodze do końcowego wyniku.
- Rozwiązanie:
Wzór na objętość graniastosłupa:
$$V_{g}=P_{p}\cdot H$$Wzór na objętość ostrosłupa:
$$V_{o}=\frac{1}{3}P_{p}\cdot H$$Podstawmy teraz do wzoru na objętość ostrosłupa objętość z treści zadania:
$$81\sqrt{3}=\frac{1}{3}P_{p}\cdot H \quad\bigg/\cdot3 \\
243\sqrt{3}=P_{p}\cdot H$$Po prawej stronie równania otrzymaliśmy wzór na pole graniastosłupa. W związku z tym \(V_{g}=243\sqrt{3}\).
- Odpowiedź:
D. \(243\sqrt{3}\)

Oblicz objętość ostrosłupa \(ABCD\), jeżeli wiadomo, że \(|AD|=12\), \(|BC|=6\), \(|BD|=|CD|=13\).
- Rozwiązanie:
Krok 1. Stworzenie rysunku pomocniczego.
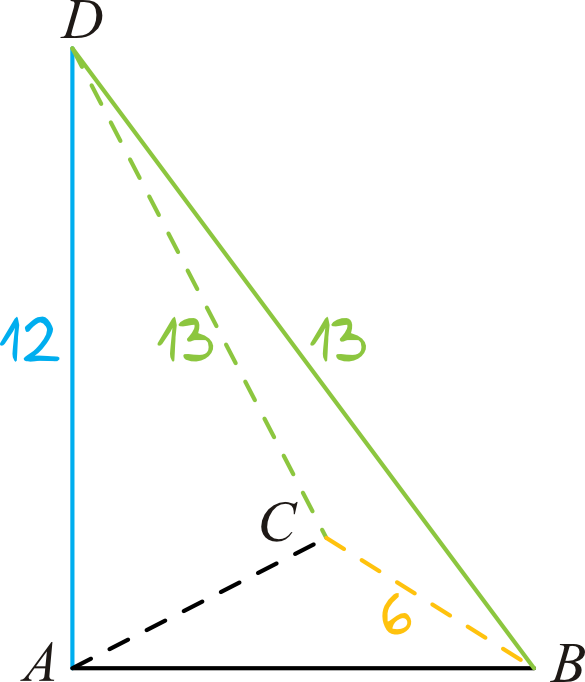
W zasadzie do obliczenia objętości brakuje nam tylko pola podstawy, bo wysokość bryły już znamy. Aby obliczyć to pole to potrzebna byłaby wysokość trójkąta, który znalazł się w podstawie. Wyliczymy ją bez problemu jeśli poznamy długości boków \(AB\) i \(AC\) i właśnie od tego rozpoczniemy obliczenia.
Krok 2. Obliczenie długości boków \(AB\) i \(AC\).Skorzystamy tutaj z Twierdzenia Pitagorasa. Aby obliczyć bok \(AB\) wystarczy wziąć do obliczeń duży trójkąt \(ABD\), którego miary dwóch boków są nam znane, a więc:
$$a^2+b^2=c^2 \\
|AB|^2+|AD|^2=|BD|^2 \\
|AB|^2+12^2=13^2 \\
|AB|^2+144=169 \\
|AB|^2=25 \\
|AB|=5 \quad\lor\quad |AB|=-5$$(wartość ujemną odrzucamy, bo bok nie może mieć długości ujemnej)
Długość boku \(AC\) wyliczymy dokładnie w ten sam sposób, tyle tylko że skorzystamy z trójkąta \(ACD\). Jego wymiary są identyczne co trójkąta \(ABD\) (są to więc trójkąty przystające), a więc i bok \(AC\) ma długość \(5\).
Krok 3. Obliczenie długości wysokości trójkąta \(ABC\).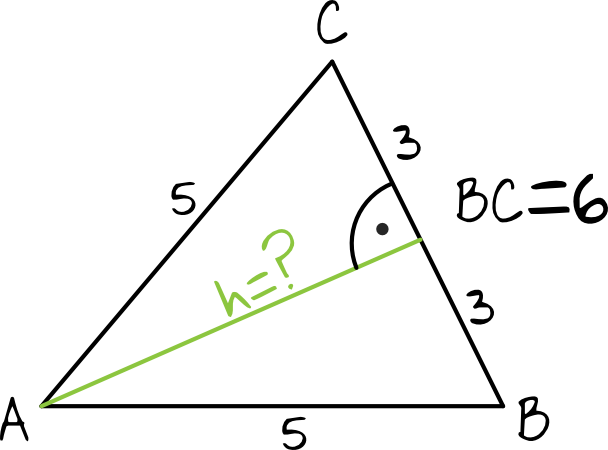
W podstawie mamy trójkąt równoramienny, a więc jego wysokość podzieli nam bok \(BC\) na dwie równe części. Wysokość trójkąta wyliczymy więc używając ponownie Twierdzenia Pitagorasa.
$$a^2+b^2=c^2 \\
h^2+|CE|^2=|AC|^2 \\
h^2+3^2=5^2 \\
h^2+9=25 \\
h^2=16 \\
h=4 \quad\lor\quad h=-4$$(wartość ujemną oczywiście odrzucamy)
Krok 4. Obliczenie pola podstawy trójkąta znajdującego się w podstawie.$$P_{p}=\frac{1}{2}a\cdot h \\
P_{p}=\frac{1}{2}\cdot6\cdot4 \\
P_{p}=12$$Krok 5. Obliczenie objętości ostrosłupa.Znając już wszystkie potrzebne miary możemy bez problemu obliczyć objętość ostrosłupa:
$$P_{p}=12 \\
H=12 \\
V=\frac{1}{3}\cdot P_{p}\cdot H \\
V=\frac{1}{3}\cdot12\cdot12=48$$ - Odpowiedź:
Objętość ostrosłupa jest równa \(48\).
35. Bryły obrotowe
Podpowiedź: Kiedy mamy narysowany przekrój stożka lub walca, to wysokość stożka/walca dzieli nam dolną krawędź na dwie równe części, gdzie każda z nich ma długość równą promieniowi okręgu znajdującego się w podstawie. Pamiętaj też, że jedną z częstszych pułapek jest podawanie w treści zadania długości średnicy, a nie promienia (a to promień jest nam potrzebny do wyliczania np. objętości).
Ostatnia deska ratunku: Jeżeli na przekroju kąt między tworzącą stożka i promieniem podstawy ma miarę \(45°\), to trójkąt składający się z wysokości trójkąta, promienia i tworzącej stożka jest trójkątem prostokątnym równoramiennym.
- Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
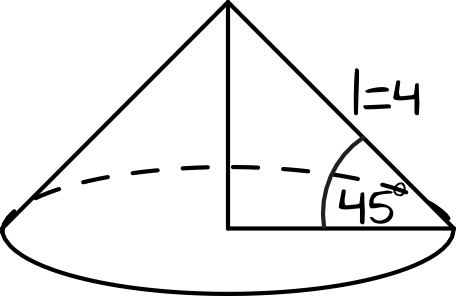
Widzimy, że promień, wysokość oraz tworząca stożka utworzyły nam trójkąt prostokątny \(ABC\). Znamy tylko długość tworzącej stożka oraz miarę kąta jej nachylenia do podstawy, więc chcąc obliczyć wysokość stożka musimy skorzystać albo z własności trójkątów \(45°, 45°, 90°\) albo z trygonometrii.
Krok 2. Obliczenie wysokości stożka.Korzystając z zasad trygonometrii otrzymamy:
$$sin45°=\frac{h}{l} \\
\frac{\sqrt{2}}{2}=\frac{h}{4} \\
h=2\sqrt{2}$$ - Odpowiedź:
A. \(2\sqrt{2}\)
- Rozwiązanie:
Do wzoru na objętość stożka potrzebujemy znać długość promienia podstawy. W treści zadania mamy podaną średnicę, zatem:
$$r=12:2=6$$Teraz możemy podstawić wszystkie dane z treści zadania (\(r=6\), \(H=4\)) i obliczyć poszukiwaną objętość:
$$V=\frac{1}{3}πr^2 H \\
V=\frac{1}{3}π\cdot6^2\cdot4 \\
V=\frac{1}{3}π\cdot36\cdot4 \\
V=\frac{1}{3}π\cdot144 \\
V=48π$$ - Odpowiedź:
D. \(48π\)
36. Średnia arytmetyczna, mediana i inne
Podpowiedź: Pamiętaj, że zanim zaczniemy liczyć medianę to trzeba uszeregować liczby od najmniejszej do największej.
Ostatnia deska ratunku: Jeżeli liczba wyrazów jest nieparzysta, to mediana nie może być liczbą, której nie ma w zbiorze.
- Rozwiązanie:
Krok 1. Uporządkowanie wyników rzutu kostką.
Aby obliczyć medianę musimy najpierw ustawić wyniki z rzutów w porządku niemalejącym, zatem:
$$1,3,4,6$$Krok 2. Obliczenie mediany.W przypadku ciągu, który ma nieparzystą liczbę elementów, medianą jest środkowy wyraz. Nasz ciąg ma jednak parzystą liczbę elementów (dokładnie cztery), a więc aby uzyskać medianę musimy obliczyć średnią arytmetyczną dwóch środkowych wyrazów. W naszym przypadku środkowymi wyrazami są \(3\) oraz \(4\), tak więc mediana będzie równa:
$$m=\frac{3+4}{2}=3,5$$ - Odpowiedź:
D. \(3,5\)
- Rozwiązanie:
Krok 1. Obliczenie wartości niewiadomej \(x\).
Zanim obliczymy medianę musimy poznać wartość niewiadomej \(x\). Zrobimy to układając proste równanie związane ze średnią arytmetyczną:
$$\frac{x+13+7+5+5+3+2+11}{8}=7 \\
\frac{x+46}{8}=7 \quad\bigg/\cdot8 \\
x+46=56 \\
x=10$$Krok 2. Uporządkowanie liczb i wyznaczenie mediany.Zanim zaczniemy obliczać medianę musimy uporządkować liczby w porządku niemalejącym:
$$2,3,5,5,7,10,11,13$$Mamy parzystą liczbę wyrazów, więc medianę wyznaczymy w następujący sposób:
$$m=\frac{5+7}{2} \\
m=\frac{12}{2} \\
m=6$$ - Odpowiedź:
A. \(6\)
37. Obliczanie ilości kombinacji
Podpowiedź: Zawsze zwracaj uwagę na to, czy dane liczby (lub inne zdarzenia) mogą się powtarzać, czy też nie. Czasem trzeba wywnioskować to z treści zadania, czasem będzie to zapisane wprost i będzie użyty zwrot „ze zwracaniem” lub „bez zwracania”.
Ostatnia deska ratunku: Jeżeli chcesz wypisać sobie jakieś kombinacje, to nie rozpisuj zdarzeń chaotycznie, tylko ustal sobie jakąś regułę wypisywania.
- Rozwiązanie:
Zadanie można policzyć na dwa sposoby.I sposób – korzystając z tzw. reguły mnożenia.Wybierając pierwszego gracza dokonujemy wyboru spośród \(10\) zawodników.
Wybierając drugiego gracza dokonamy wyboru już tylko spośród \(9\) zawodników.
To dałoby nam łączną liczbę kombinacji równą \(10\cdot9=90\), ale to niestety nie jest koniec zadania. Musimy jeszcze zauważyć, że w ten sposób niejako zdublowały nam się poszczególne pary. Przykładowo wybór Lewandowski-Grosicki jest tym samym co wybór Grosicki-Lewandowski, a według tego co obliczyliśmy przed chwilą byłyby to dwie oddzielne kombinacje. Dlatego też musimy jeszcze nasze \(90\) kombinacji podzielić na \(2\) i tak oto otrzymamy odpowiedź, że możemy naszych zawodników wybrać na \(4\)5 sposobów.II sposób – korzystając ze wzoru na liczbę kombinacji.$$C_{10}^2=\binom{10}{2}=\frac{10!}{(10-2)!\cdot2!}=\frac{8!\cdot9\cdot10}{8!\cdot2}=\frac{90}{2}=45$$
- Odpowiedź:
C. \(45\)
- Rozwiązanie:
Krok 1. Określenie liczby cyfr, które mogą znaleźć się na pierwszym miejscu naszej liczby.
Zgodnie z treścią zadania pierwsza cyfra musi być parzysta, a więc mogą to być tylko i wyłącznie \(2\), \(4\), \(6\) lub \(8\). Cyfrę \(0\) odrzucamy, bo nie może być pierwszą cyfrą w liczbie.
Krok 2. Określenie liczby cyfr, które mogą znaleźć się na drugim, trzecim i czwartym miejscu naszej liczby.Na każdym z pozostałych miejsc możemy mieć jedną z pięciu cyfr nieparzystych: \(1\), \(3\), \(5\), \(7\) lub \(9\).
Krok 3. Obliczenie liczby wszystkich możliwych kombinacji.Zgodnie z regułą mnożenia wszystkich kombinacji będzie:
$$|Ω|=4\cdot5\cdot5\cdot5=500$$ - Odpowiedź:
\(500\) liczb.
38. Obliczanie prawdopodobieństwa
Podpowiedź: Zwróć uwagę na to, czy proszą nas w treści zadania o wyliczenie prawdopodobieństwa np. wylosowania liczby \(3\), czy też liczb większych od \(3\). Albo czy mamy policzyć prawdopodobieństwo wyrzucenia dwóch reszek, czy też przynajmniej dwóch reszek. Naprawdę wiele osób źle rozwiązuje zadanie właśnie ze względu na niedoczytanie warunków zadania.
Ostatnia deska ratunku: Czasem najlepszym sposobem na obliczenie ilości np. zdarzeń sprzyjających jest po prostu wypisanie sobie wszystkich możliwości.
- Rozwiązanie:
Krok 1. Ustalenie liczby wszystkich możliwych zdarzeń elementarnych.
Na każdej kostce mamy sześć możliwości, rzuty kostek są względem siebie niezależne, więc liczba możliwych kombinacji przy rzucie dwoma kostkami jest równa:
$$|Ω|=6\cdot6=36$$Krok 2. Ustalenie liczby zdarzeń sprzyjających.Zgodnie z treścią zadania wiemy, że zdarzeniami sprzyjającymi są te, których suma oczek jest równa trzy. Mamy tylko dwie takie możliwości: \((2;1)\) oraz \((1;2)\). Tak więc \(|A|=2\).
Krok 3. Obliczenie prawdopodobieństwa.Prawdopodobieństwo obliczymy korzystając ze wzoru:
$$P(A)=\frac{|A|}{|Ω|}=\frac{2}{36}=\frac{1}{18}$$ - Odpowiedź:
D. \(\frac{1}{18}\)
- Rozwiązanie:
Krok 1. Obliczenie liczby wszystkich zdarzeń elementarnych.
Rzucając monetą mamy dwie możliwości otrzymania wyniku – wypadnie nam orzeł \((O)\) lub reszka \((R)\). W każdym z trzech rzutów będziemy mieć identyczną sytuację, więc zgodnie z regułą mnożenia wszystkich zdarzeń elementarnych (czyli różnych kombinacji otrzymanego wyniku) będziemy mieć:
$$|Ω|=2\cdot2\cdot2=8$$Krok 2. Obliczenie liczby zdarzeń sprzyjających.Zdarzeniem sprzyjającym jest w naszym przypadku taka kombinacja trzech rzutów, w których choć raz pojawi się reszka np. \(ROO, RRO, ORO\) itd. Możemy wypisać sobie wszystkie te kombinacje, ale wystarczy zauważyć, że jest tylko jedna jedyna możliwość, kiedy takiej reszki nie będzie. To będzie rzut \(OOO\). Wszystkie pozostałe zawierają choć jedną reszkę. Zatem zdarzeń sprzyjających mamy:
$$|A|=8-1=7$$Krok 3. Obliczenie prawdopodobieństwa.$$P(A)=\frac{|A|}{|Ω|}=\frac{7}{8}$$
- Odpowiedź:
A. \(\frac{7}{8}\)


Super materiały, bardzo mi pomagają i uczę się ostro teraz ;) Szanuję i podziwiam za poświęconą ilość czasu na przygotowanie tego wszystkiego. Mam taki pomysł, może zrobić jakieś małe zestawienie wzorów których nie ma w tablicach a które trzeba umieć? Pozdrawiam ;)
Dzięki za miłe słowa! Co do wzorów spoza tablic, to pomysł jest dobry, choć tych wzorów tak prawdę mówiąc za wiele nie ma. Może wypiszę je tutaj bezpośrednio, a w przyszłości pomyślę jak to jeszcze lepiej oprawić ;) Na pewno trzeba znać: – wzory na błąd bezwzględny i względny (jest do nich link w treści tych pewniaków gdzie omawiam te błędy) – teoretycznie wzorem można nazwać zależności w kwadracie (czyli że przekątna kwadratu o boku a ma długość a√2) oraz zależności w trójkącie równobocznym, gdzie wysokości tego trójkąta przecinają się w stosunku 2:1 (czyli od wierzchołka trójkąta do miejsca przecięcia… Czytaj więcej »
może jeszcze a√3 na przekątną sześcianu, bardzo rzadko, ale widziałem, ze się przydaje
Bardzo dobra sugestia :)
Ja osobiście bym dodał dokładny wzór na Ostrosłup prawidłowy trójkątny, czyli Pole i Objętość.
Bardzo dobra robota, miła niespodzianka na dwa dni przed maturą z matematyki! Pozdrawiam:)
super strona i świetnie wyjaśnione zadania. Będą w przyszłości matury rozszerzone ?
Nie mówię „nie”, aczkolwiek matura rozszerzona to pieśń przyszłości, bo jest jeszcze sporo innych rzeczy które chcę zrobić :)
super mimo rozwiązania wszystkich matur do 2013 to jest to fajny sposób na powtórkę przed maturą. Dzięki, jednak rozwiązywanie matur najwięcej uczy
to chyba jednak metoda na „ostatnią godzinę” i możliwość sprawdzenia swoich umiejętności / braków :)
Dziękuję za calutki kurs i za te pewniaki!!! Nie wiem, czy Pan zna to uczucie (pewno nie, bo Pan matmę umie), kiedy z niemalże zerowego pojęcia o matematyce udaje się zaliczyć arkusze online na prawie 50%. Przysięgam, po dwóch tygodniach „romansu” (=D) z Panem i matematyką wiem więcej niż po 4 latach w technikum. Skończyłam te pewniaki i nic bardziej nie zadowala i nie motywuje jak poprawnie rozwiązane przeze mnie zadania. Dziękuję bardzo jeszcze raz. Pozdrawiam!
I to się nazywa mega pozytywna wiadomość! Wielkie dzięki za wspólną naukę i trzymam kciuki na jutrzejszym egzaminie, będzie dobrze :)
PS. I jaki ja tam Pan, ja niewiele starszy od Was jestem :D
Dziękuję bardzo za poświęcony czas. Materiały wspaniałe, jutro maturka, a ja właśnie skończyłam rozwiązywać zadanka:).
Jakość materiałów maturalnych na tej stronie jest rewelacyjna, a te pewniaki są wręcz wisienką na torcie. Kurs, arkusze oraz pewniaki i nagle się okazuje, że matura jest prosta ;)
ta strona jest niesamowita! szczerze przyznam, że też przygotowuję znajomą do matematyki, ale chyba od razu skieruję ją na tę stronę. to idealne kompendium jak na pewno zdać maturę z matmy
Ta strona naprawdę pomaga mi w przygotowywaniu do matury. Robię arkusze, sprawdzam od razu rozwiązania jeśli czegoś nie rozumiem, przypominam sobie pewniaki maturalne. Dziękuję za tę stronę!
Bardzo przydatne materiały niektóre zadania były lekko niezrozumiałe ale po krótkim zastanowieniu od razu wiedziałem o co chodzi.
Bardzo pomocne materiały, dużo moich znajomych również korzysta i tez sobie bardzo chwalą. Fajnie wytłumaczone, wszystko czytelne, matematyka wydaje się nieco prostsza. Teraz matemaks poszedł w odstawkę.
Mega! bardzo dziękuję za poświęcony czas i szczegółowe wyjaśnienia. pozdrawiam
Świetna strona! Cieszę się, że ją znalazłam, bardzo mi pomaga w przygotowaniu się do matury. Dodam, że z matematyki jestem kompletnie zielona, a dzięki tej stronie bardziej ją zrozumiałam. Pozdrawiam!!!
Monotoniczność ciągów jest istotna na maturze? Może trafić się takie zadanie?
Prawdę mówiąc, to jest dość istotna w konkretnych typach zadań. Bardzo często jest tak, że w trakcie obliczeń (zwłaszcza w ciągu geometrycznym) wyjdą nam dwie możliwości i wtedy informacja o tym, że ciąg jest np. rosnący, ma wpływ na to, że coś trzeba odrzucić :)
Dzięki!
Czy wszystkie te zadania obowiązują na maturę 2021 czy coś można pominąć? Ciężko mi samej niestety rozróżnić co będzie a co nie… :( Bardzo proszę o wskazówkę, zostało mało czasu a ja czuję się bardzo niepewnie, chciałabym zrobić sobie te pewniaki ale nie wiem na co nie tracić czasu
Jeżeli jakieś zagadnienie wypadło z matury 2021, to pod danym punktem jest odpowiednia adnotacja :) Dałem teraz lepsze ramki, tak aby wszystko było bardziej widoczne :)
Dziękuję za te ramki i zabieram się do roboty! :)
Czy przerabiając podpunkty 1-21 i 36-38 jestem w stanie zdać na 30%? Chodzi mi o pominięcie punktów 22-35, ze względu na moją ułomność w temacie geometrii
Jeżeli te tematy opanowałeś/aś dość dobrze (czyli naprawdę umiesz rozwiązywać zadania z nierównościami, funkcjami, ciągami itd.) to myślę, że zdasz bez problemu :)
mam pytanko skąd w zadaniu 3 z ułamkiem wzięło się na górze 4 pod pierwiastkiem 5 ? :?
To jest 5 do potęgi 4 razy pierwiastek z 5, więc ta czwórka jest w wykładniku potęgi liczby 5, a nie stopniem pierwiastka ;)
Fantastyczny artykuł, nie znam lepszego! Bardzo dziękuję za pomoc w przygotowaniu do matury i update dla 2021r. ;) to bardzo pomocne, przejrzyste i miłe.
Idealna szybka powtórka na parę dni przed maturą z matematyki! Wszystko dobrze wyjaśnione i widać, że jest to kawał dobrej roboty ;)
dzięki, może zdam maturę
przygotowuję się z panem do matury już od dawna i serdecznie polecam tę stronę wszystkim moim znajomym, mam nadzieję, że zdobyta wiedza sprawi, iż mój wynik będzie kosmiczny;)
Dziękuję, za dwa dni matura i cały rok uczyłam się właśnie z tą stroną. Na początku, pierwsza próbna matura na 34% a w weekend napisana na 76%. Jesteś niesamowity i jestem bardzo wdzięczna za to co tworzysz
I pięknie! O to właśnie chodzi – krok po kroczku poprawiłaś swoje umiejętności i teraz matura będzie już znacznie mniej stresująca, a i można będzie się poduczyć jeszcze czegoś z innych przedmiotów :) Trzymam kciuki!
W środę pisze maturę poraz 3… dziękuję bardzo za ten zestaw zadań właśnie go skończyłam zajęło mi to cały dzień ale dużo sobie w głowie ułożyłam
Mam nadzieję że tym razem zdam
Pochodzę do matury czwarty raz, mam nadzieję, ze po przerobieniu wszystkich zadań z działów co już zrobiłam nic mnie nie zaskoczy
Skąd 12x w podpunkcie 20b ?
Wzory skróconego mnożenia! (a+b)^2=a^2+2ab+b^2, więc analogicznie (2x+3)^2=4x^2+12x+9 :)
Super materiały, bardzo mi pomagają i uczę się ostro teraz ;) Szanuję i podziwiam za poświęconą ilość czasu na przygotowanie tego wszystkiego. Mam taki pomysł, może zrobić jakieś małe zestawienie wzorów których nie ma w tablicach a które trzeba umieć? Pozdrawiam ;)\
W jednym z komentarzy powyżej właśnie o tym rozmawiałem z inną osobą i tam wypisałem takie wzorki ;)
znakomity materiał, dziękuję bardzo
dziękuje za proste wyjaśnienia
W zadaniu 34 z ostrosłupem skąd wiadomo że jest prostokątny ? Nigdzie nie ma zaznaczonego kąta? Czy to wynika z jakiejś własności ?
W treści zadania masz informację, że krawędź AD jest wysokością tej bryły i stąd wiemy, że trójkąty ABD oraz ACD są prostokątne :)
super strona i super pomysł i wykonanie pogratulować tylko (żebyście tylko nie wpadli na pomysł zrobienia strony płatnej bo odstraszy to wielu) ;)
Fantastyczny materiał do nauki ja i wszyscy maturzyści dziękujemy
Czyli jeżeli zrobiłem wszystkie te pewniaki bez problemu to zdam? :D
Zdecydowanie tak, pod warunkiem, że na prawdę umiesz rozwiązywać tego typu zadanka :)
bardzo fajnie przygotowane krótko i na temat dzięki wielkie
Jesteś Radku niemożliwy.
Dzięki Tobie, twoim nagraniom i Matbrykowi wreszcie uporządkowałem sobie całą matematyczną wiedzę i myślę że dam radę na maturze. Choć nie uważam się za orła(za mało godzin spędzonych z powyższymi pomocami) ale mam nadzieję że z moich 15% sprzed kursu dojdę do co najmniej 40%.
Pozdrawiam! Tak trzymaj!
Na pewno wszystko będzie w porządku i już jutro dołączysz do grona tych, którzy będą dobrze wspominać zmagania maturalne z matematyki :) Trzymam kciuki za jak najlepszy wynik i przy okazji dziękuję Ci za udział w kursie i za zakup Matbryka :)
dziekuwa mordzia fajne zadanka super powtóra wiesz co jest 5 pozdro wszystkim przed maturka
Żaden kanał na Youtube ani strona internetowa nie pomogła mi w przygotowaniu do matury jak Szalone Liczby! Zadania są prosto i zrozumiale wytłumaczone. Dziękuję bardzo za pomoc! Jutro walczę <3
Miło mi to czytać, bardzo dziękuję za te słowa :) Cieszę się, że mogłem choć trochę pomóc w przygotowaniach, no i trzymam mocno kciuki za jutrzejszą batalię! :)
W punkcie 17. w zadaniu z przesunięciem funkcji jest błąd. Powinno być (x+2) a nie (×-2).
Straciłem dzisiaj jeden punkt na maturze przez to :)
Ale tam jest właśnie dobrze, tak więc i na maturze musisz mieć ok! Jak funkcja jest przesunięta w prawo, to mamy (x-2), a jakby była w lewo, to mielibyśmy (x+2) :) Przesunięcia w lewo/prawo są właśnie nieintuicyjne, to standardowy dylemat uczniów :)
Dzięki szaloneliczby.pl moje dzieci przygotowały się do egzaminu ósmoklasisty, teraz szykują się do matury, zaliczyły kilka lat w edukacji domowej ucząc się matematyki właściwie tylko tutaj. Jestem pod ogromnym wrażeniem ilości materiału, przystępnego tłumaczenia, ciekawych quizów i dobrze zrobionych sprawdzianów. Bardzo dziękuję :)
I to mi się podoba, pozytywna energia! Nie pozostaje mi nic innego jak życzyć dzieciom jak najlepszych wyników na maturze! :)
Bardzo ładnie opracowane zadania, super
Świetna strona, właśnie czegoś takiego potrzebowałam :D Dziękuję!!
Cześć, ciągle nie potrafię pojąć, kiedy przedział rozwiązań nierówności będzie „wewnątrz” paraboli, a kiedy „na zewnątrz”. Na przykład zadanie 11, punkt drugi
(2x−3)(3−x)≥0
Dlaczego tutaj przedział to x∈⟨1,5;3⟩ a nie x∈(−∞;1,5⟩∪⟨3;+∞) ?
To jedne z moich ostatnich pytań przed jutrem i jeśli jutro zdam, to już więcej nie będę Panu zawracał głowy :)
W tym konkretnym zadaniu szukamy argumentów dla których przyjmowana jest wartość większa lub równa 0. Patrzymy się zatem na parabolę i na to, co znajduje się nad osią OX oraz na tej osi. Mówiąc bardzo obrazowo, interesuje nas ten „pagórek”, który ciągnie się od x=1,5 aż do x=3. Stąd też właśnie rozwiązaniem jest tutaj przedział od 1,5 do 3 (z nawiasami domkniętymi) :)
zdałam maturę dzięki!
Czy jest dla mnie jakaś nadzieja, jeśli z zerowym poziomem wiedzy, zacznę uczyć się tych i podobnych pewniaków (a mamy grudzień)?:D
Zerowego poziomu wiedzy to nie masz na pewno :D Ale potwierdzam, że nawet będąc słabym z matematyki można w kilka miesięcy się przygotować i zdać na spokojnie maturę z matematyki. Od lat mam takich uczniów pod swoimi skrzydłami w ramach kursu maturalnego, więc nie rzucam słów na wiatr ;) A kurs o którym mówię znajduje się tutaj: https://szaloneliczby.pl/kurs-maturalny-matematyka-poziom-podstawowy/
Ważne pytańko – Napisałam próbną maturę na 24% niestety, kupiłam pana kurs jak i staram się uczyć schematów tego ale w jaki sposób? Czy można też prosić o radę co zrobić w te 29 dni by mieć te 30 %? zależy mi na zdaniu i staram się uczyć choć dwie godziny jeśli nie mam czasu czasem więcej, czy jest szansa liczyć na to że w miesiąc z 24% zrobię do 30/35%? Na czym się najbardziej skupić ? Byłabym bardzo wdzięczna za odpowiedz. Pozdrawiam !!!
Dosłownie wczoraj otrzymałem wiadomość od jednej z Kursantek, która z poziomu niższego niż Twój wskoczyła na 60%, więc na spokojnie to się wszystko da ogarnąć! Najlepiej jest najpierw obejrzeć lekcję video (ale tak uczciwie, ze zrozumieniem) i potem rozwiązać przynajmniej kilka zadań ze zbioru do którego link jest zawsze pod lekcją. Czasu faktycznie nie jest dużo, więc pomijałbym te tematy trudniejsze i rzadziej pojawiające się na maturze, a skupiałbym się na pewno na: potęgach/pierwiastkach, równaniach i nierównościach kwadratowych, funkcji kwadratowej no i trygonometrii. To chyba taka najważniejsza baza do skutecznego zdania matury i to nie na 30-35%, a wręcz na… Czytaj więcej »
Super dziękuję bardzo z radę! Mam nadzieję że będę mogła podzielić się dobrymi wieściami później. Pozdrawiam
Chcę na wstępie zaznaczyć że bardzo rzadko coś komentuje, ale tym razem nie dam rady się powstrzymać! Dziękuję jako maturzysta za to co robisz. Najlepsza strona do nauki !! Wszystko jasno wytłumaczone, widać że są to zadania typowo maturalne, użyteczne pod kątem matury i zebrane w jedno miejsce. Naprawdę wow.