Rozwiązanie
Krok 1. Ułożenie i rozwiązanie układu równań.
Ze wzoru prostej oraz równania okręgu możemy ułożyć następujący układ równań:
$$\begin{cases}
y=x+4 \\
(x+1)^2+(y-2)^2=25
\end{cases}$$
Podstawiając pierwsze równanie do drugiego otrzymamy:
$$(x+1)^2+(x+4-2)^2=25 \\
(x+1)^2+(x+2)^2=25 \\
x^2+2x+1+x^2+4x+4=25 \\
2x^2+6x-20=0 \quad\bigg/:2 \\
x^2+3x-10=0$$
Krok 2. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=1,\;b=3,\;c=-10\)
$$Δ=b^2-4ac=3^2-4\cdot1\cdot(-10)=9-(-40)=9+40=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-3-7}{2\cdot1}=\frac{-10}{2}=-5 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-3+7}{2\cdot1}=\frac{4}{2}=2$$
Krok 3. Zapisanie współrzędnych przecięcia się prostej z okręgiem.
Otrzymaliśmy dwie współrzędne iksowe, bo i nasza prosta (zgodnie z treścią zadania) przecina okrąg w dwóch miejscach. To oznacza, że pierwsza współrzędna iksowa należy do punktu \(A\), natomiast druga współrzędna należy do punktu \(B\). Musimy jeszcze obliczyć współrzędne igrekowe, a zrobimy to podstawiając współrzędne iksowe do równania prostej \(y=x+4\):
Dla \(x=-5\):
\(y=-5+4\)
\(y=-1\)
Dla \(x=2\):
\(y=2+4=6\)
To nam daje następujące współrzędne:
$$A=(-5;-1),\;B=(2;6)$$
Krok 4. Obliczenie długości promienia.
Równanie okręgu o środku w punkcie \(S=(a;b)\) oraz promieniu \(r\) przyjmuje postać:
$$(x-a)^2+(y-b)^2=r^2$$
Teraz do tej postaci możemy przyrównać równanie z treści zadania. W naszym równaniu z treści zadania po prawej stronie znalazła się wartość \(25\), zatem jest to nasze \(r^2\). Możemy więc zapisać, że:
$$r^2=25 \\
r=5 \quad\lor\quad r=-5$$
Ujemne rozwiązanie oczywiście odrzucamy, bo promień nie może być ujemny.
Krok 5. Sporządzenie rysunku pomocniczego i zapisanie długości boków \(AS\) oraz \(BS\).
Z równania okręgu możemy wprost odczytać, że współrzędne środka okręgu to \(S=(-1;2)\). Ta informacja w połączeniu z obliczeniami z kroków poprzednich, czyli długość promienia \(r=5\) oraz współrzędne punktów \(A=(-5;-1),\;B=(2;6)\) pozwoli nam stworzyć następujący rysunek pomocniczy:
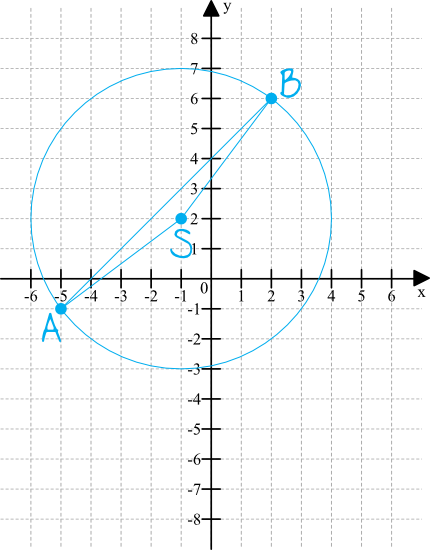
Z rysunku dość jasno wynika, że odcinki o długości \(AS\) oraz \(AB\) są równe długości promienia, zatem możemy zapisać, że:
$$|AS|=5 \\
|BS|=5$$
Krok 6. Obliczenie długości odcinka \(AB\).
Skorzystamy ze wzoru na długość odcinka w układzie współrzędnych, ponieważ znamy współrzędne punktów \(A\) oraz \(B\).
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2} \\
|AB|=\sqrt{(2-(-5))^2+(6-(-1))^2} \\
|AB|=\sqrt{7^2+7^2} \\
|AB|=\sqrt{49+49} \\
|AB|=\sqrt{49\cdot2} \\
|AB|=7\sqrt{2}$$
Krok 7. Obliczenie długości obwodu.
Mamy już wszystkie niezbędne informacje, zatem możemy bez problemu obliczyć długość obwodu:
$$Obw=5+5+7\sqrt{2}=10+7\sqrt{2}$$