Pole prostokąta ABCD jest równe 90. Na bokach AB i CD

Pole prostokąta $ABCD$ jest równe $90$. Na bokach $AB$ i $CD$ wybrano – odpowiednio – punkty $P$ i $R$, takie, że $\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}$ (zobacz rysunek).

Pole czworokąta $APCR$ jest równe:

A. $36$

B. $40$

C. $54$

D. $60$

Rozwiązanie

Krok 1. Sporządzenie rysunku pomocniczego.
Z informacji o tym, że $\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}$ wynika, że odcinki $AP$ oraz $RC$ mają długość $3x$, natomiast $PB$ oraz $RD$ mają długość $2x$:
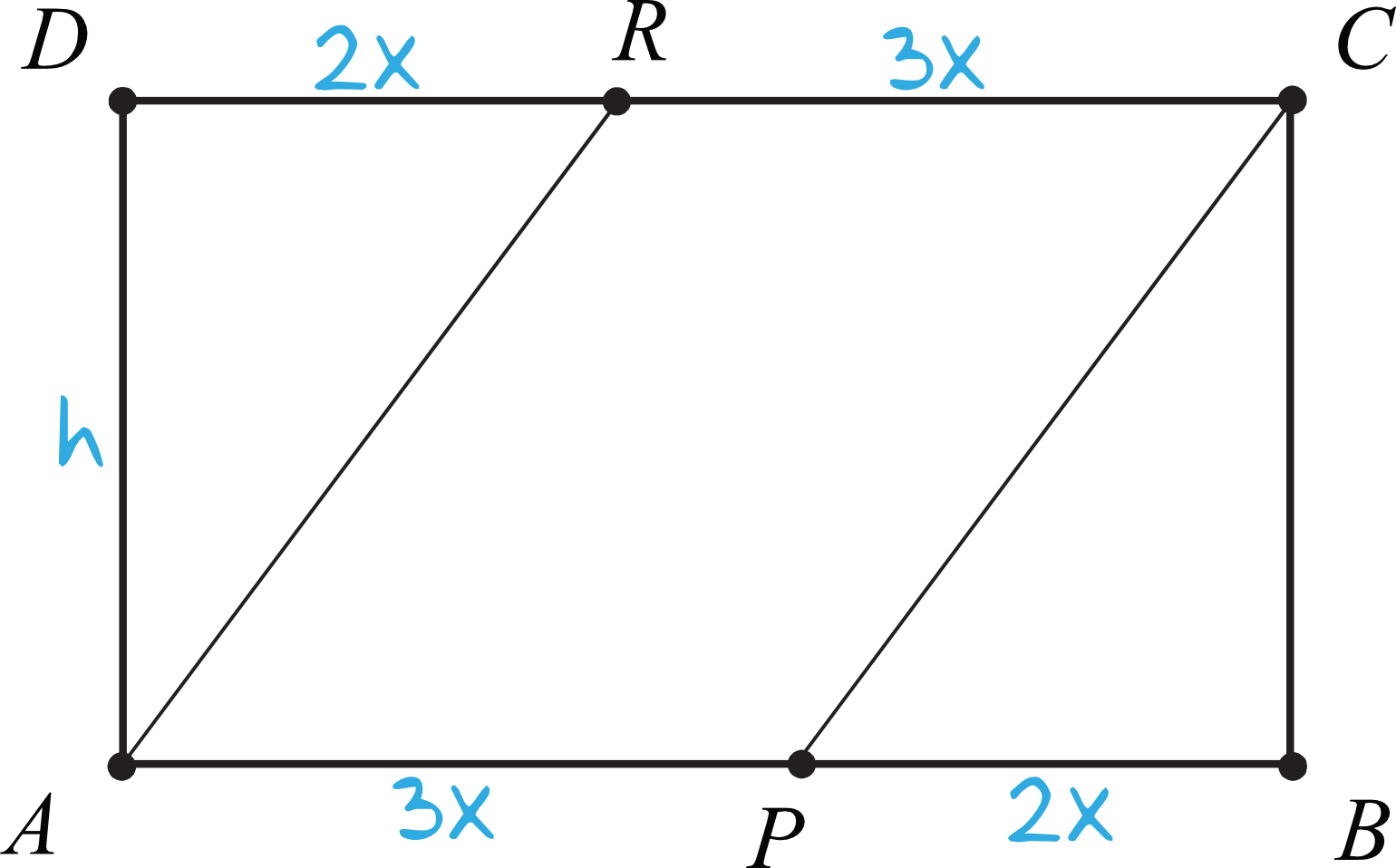
matura z matematyki

Dodatkowo na rysunku możemy sobie zaznaczyć, że odcinek $AD$ jest wysokością $h$.

Krok 2. Obliczenie pola powierzchni czworokąta $APCR$.
Z treści zadania wiemy, że prostokąt $ABCD$ o boku $|AB|=5x$ i wysokości $|AD|=h$ miał pole powierzchni równe $90$. Możemy zatem zapisać, że:
$$5x\cdot h=90 \\
h=\frac{90}{5x}$$

Nasz równoległobok $APCR$ będzie miał pole równe:
$$P=3x\cdot h$$

Podstawiając wyznaczone przed chwilą $h=\frac{90}{5x}$ otrzymamy:
$$P=3x\cdot\frac{90}{5x} \\
P=\frac{270}{5} \\
P=54$$

Odpowiedź

Zadania

Pole prostokąta ABCD jest równe 90. Na bokach AB i CD

Pole prostokąta \(ABCD\) jest równe \(90\). Na bokach \(AB\) i \(CD\) wybrano – odpowiednio – punkty \(P\) i \(R\), takie, że \(\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}\) (zobacz rysunek).

Pole czworokąta \(APCR\) jest równe:

Pole prostokąta \(ABCD\) jest równe \(90\). Na bokach \(AB\) i \(CD\) wybrano – odpowiednio – punkty \(P\) i \(R\), takie, że \(\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}\) (zobacz rysunek). Pole czworokąta \(APCR\) jest równe:

Pole prostokąta \(ABCD\) jest równe \(90\). Na bokach \(AB\) i \(CD\) wybrano – odpowiednio – punkty \(P\) i \(R\), takie, że \(\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}\) (zobacz rysunek).

Pole czworokąta \(APCR\) jest równe: