Rozwiązanie
Pole powierzchni bocznej walca wyliczymy ze wzoru:
$$P_{b}=2πrH$$
Pole podstawy wyliczymy ze wzoru:
$$P_{p}=πr^2$$
Skoro w walcu mamy dwie podstawy (dolną i górną), a pole powierzchni bocznej jest \(5\) razy większe od sumy powierzchni tych podstaw to otrzymamy równanie:
$$P_{b}=5\cdot2\cdot P_{p} \\
2πrH=10\cdot πr^2 \quad\bigg/:πr \\
2H=10r \\
H=5r$$
Krok 2. Sporządzenie rysunku pomocniczego.
Nanieśmy na rysunek informację, którą przed chwilą otrzymaliśmy i zaznaczmy przy okazji poszukiwany kąt:
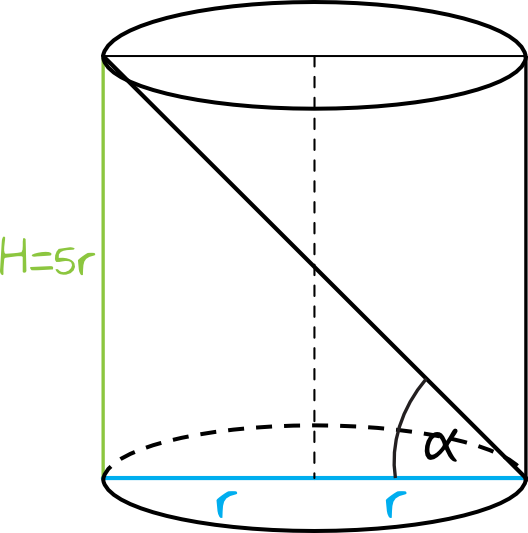
Krok 3. Obliczenie miary kąta nachylenia przekątnej przekroju osiowego walca do podstawy.
Tangens odpowiada stosunkowi długości dwóch przyprostokątnych. Jedna przyprostokątna ma długość \(5r\), druga ma długość \(2r\), zatem zgodnie z rysunkiem możemy zapisać, że:
$$tgα=\frac{5r}{2r} \\
tgα=2,5$$
Z tablic możemy odczytać, że tangens przyjmuje wartość około \(2,4751\) dla kąta o mierze \(68°\) oraz wartość około \(2,6051\) dla kąta o mierze \(69°\). Znacznie bliżej jest do tej pierwszej wartości, zatem możemy powiedzieć, że nasz poszukiwany kąt ma w przybliżeniu \(68°\).