Podstawą ostrosłupa ABCDE jest kwadrat, a spodek F wysokości EF ostrosłupa jest środkiem krawędzi AD

Podstawą ostrosłupa $ABCDE$ jest kwadrat, a spodek $F$ wysokości $EF$ ostrosłupa jest środkiem krawędzi $AD$ (patrz rysunek). Ponadto wiadomo, że każda z dwóch dłuższych krawędzi bocznych tego ostrosłupa ma długość $12\sqrt{5}cm$ i jest nachylona do płaszczyzny podstawy pod kątem $60°$. Oblicz objętość tego ostrosłupa.

Rozwiązanie

Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc na rysunek dane z treści zadania otrzymamy następującą sytuację:
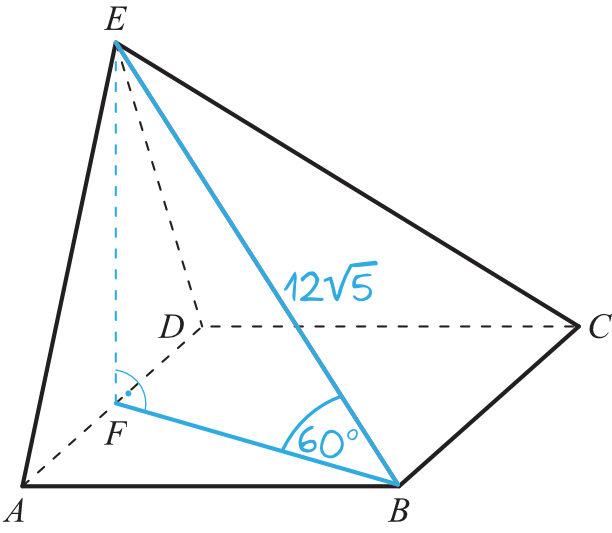
matura z matematyki

Tutaj kluczowy staje się trójkąt $EFB$, który jest trójkątem prostokątnym, a dokładniej rzecz ujmując jest to trójkąt prostokątny o kątach $30°,60°,90°$.

Krok 2. Obliczenie długości odcinków $FB$ oraz $EF$.
Spójrzmy na nasz trójkąt $EFB$. Przeciwprostokątna tego trójkąta ma długość $12\sqrt{5}$. Za pomocą funkcji trygonometrycznych lub też własności trójkątów o kątach $30°,60°,90°$ jesteśmy w stanie wyznaczyć pozostałe boki tego trójkąta. Spróbujmy może skorzystać z własności takich trójkątów i zacznijmy od wyznaczenia długości odcinka $FB$.
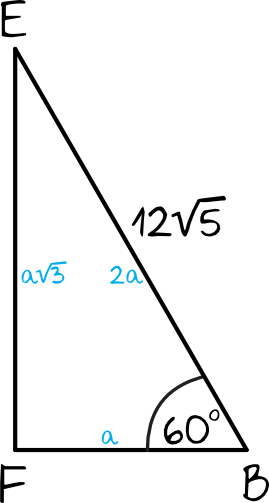
matura z matematyki

Zgodnie z własnościami trójkątów o kątach $30°,60°,90°$, odcinek $FB$ jest dwukrotnie krótszy od przeciwprostokątnej, zatem:
$$FB=12\sqrt{5}:2 \\
FB=6\sqrt{5}$$

Teraz wyznaczmy długość odcinka $EF$ (która jest jednocześnie wysokością naszego ostrosłupa). Ją moglibyśmy wyznaczyć nawet z Twierdzenia Pitagorasa, ale trzymając się własności trójkątów o kątach $30°,60°,90°$ wiemy, że ten odcinek będzie $\sqrt{3}$ razy większy od przyprostokątnej $FB$. W związku z tym:
$$EF=6\sqrt{5}\cdot\sqrt{3} \\
EF=6\sqrt{15}$$

Skoro odcinek $EF$ jest wysokością ostrosłupa, to możemy od razu zapisać, że $H=6\sqrt{15}$.

Krok 3. Obliczenie długości krawędzi podstawy.
Spójrzmy na trójkąt $ABF$. Na pewno jest to trójkąt prostokątny, bo kąt $FAB$ jest kątem kwadratu znajdującego się w podstawie.
Znamy długość przeciwprostokątnej tego trójkąta, czyli $FB=6\sqrt{5}$. Jeżeli odcinek $AB$ oznaczymy jako $a$, to odcinek $AF$ będziemy mogli zapisać jako $\frac{1}{2}a$. W związku z tym zgodnie z Twierdzeniem Pitagorasa otrzymamy:
$$a^2+\left(\frac{1}{2}a\right)^2=(6\sqrt{5})^2 \\
a^2+\frac{1}{4}a^2=36\cdot5 \\
\frac{5}{4}a^2=180 \\
a^2=144 \\
a=12 \quad\lor\quad a=-12$$

Ujemną długość oczywiście odrzucamy, zatem zostaje nam $a=12$.

Krok 4. Obliczenie objętości ostrosłupa.
Wiemy już, że w podstawie ostrosłupa jest kwadrat o boku $a=12$, a wysokość ostrosłupa to $H=6\sqrt{15}$. Znając te dane możemy przystąpić do liczenia objętości:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}a^2\cdot H \\
V=\frac{1}{3}\cdot12^2\cdot6\sqrt{15} \\
V=\frac{1}{3}\cdot144\cdot6\sqrt{15} \\
V=48\cdot6\sqrt{15} \\
V=288\sqrt{15}[cm^3]$$

Odpowiedź

$V=288\sqrt{15}cm^3$