Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
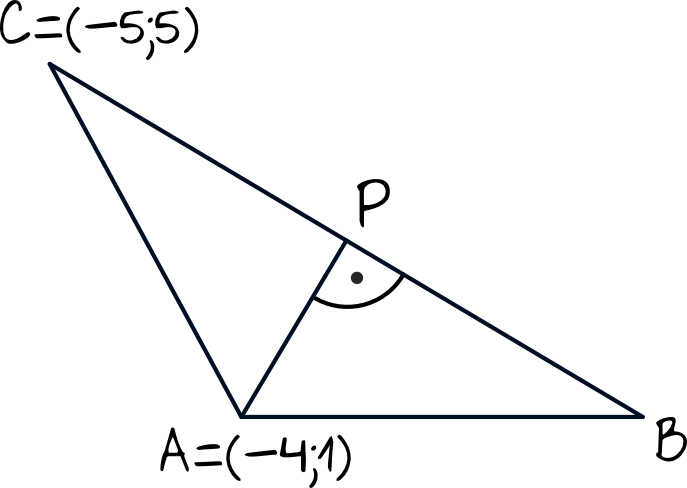
Krok 2. Wyznaczenie współczynnika \(a\) prostej \(AB\).
Prosta \(AB\) jest prostopadła do prostej \(CP\). Wiemy, że prosta \(CP\) wyraża się wzorem \(-x-y=0\), czyli \(y=-x\). Aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych \(a\) musi być równy \(-1\). Nasza prosta symetralna ma ten współczynnik równy \(-1\) (bo przed iksem nie ma żadnej liczby i stoi minus), zatem prosta \(AB\) ma ten współczynnik równy:
$$a\cdot(-1)=-1 \\
a=1$$
To oznacza, że prosta \(AB\) wyraża się wzorem \(y=1x+b\), czyli \(y=x+b\).
Krok 3. Wyznacznie współczynnika \(b\) prostej \(AB\).
Do wyznaczenia współczynnika \(b\) posłuży nam punkt \(A\), którego współrzędne mamy podane w treści zadania. Podstawiając te współrzędne do wzoru \(y=x+b\) otrzymamy:
$$1=-4+b \\
b=5$$
To oznacza, że prosta \(AB\) jest opisana wzorem \(y=x+5\).
Krok 4. Wyznaczenie współrzędnych punktu \(P\).
Punkt P jest miejscem przecięcia się dwóch prostych, których wzory są nam już znane. To oznacza, że możemy z równań tych prostych ułożyć układ równań, a rozwiązaniem tego układu będą właśnie współrzędne punktu \(P\).
$$\begin{cases}
y=-x \\
y=x+5
\end{cases}$$
Dodając równanie stronami otrzymamy:
$$2y=5 \\
y=\frac{5}{2}$$
Znamy już współrzędną igrekową, teraz musimy obliczyć współrzędną iksową, a zrobimy to podstawiając \(y=\frac{5}{2}\) do jednego z równań:
$$\frac{5}{2}=-x \\
x=-\frac{5}{2}$$
To oznacza, że \(P=\left(-\frac{5}{2};\frac{5}{2}\right)\).
Krok 5. Obliczenie długości odcinka \(AP\) i \(AB\).
Długość odcinka \(AP\) obliczymy ze wzoru na długość odcinka w układzie współrzędnych:
$$|AP|=\sqrt{(x_{P}-x_{A})^2+(y_{P}-y_{A})^2} \\
|AP|=\sqrt{\left(-\frac{5}{2}-(-4)\right)^2+\left(\frac{5}{2}-1\right)^2} \\
|AP|=\sqrt{\left(-\frac{5}{2}+4\right)^2+\left(\frac{5}{2}-1\right)^2} \\
|AP|=\sqrt{\left(\frac{3}{2}\right)^2+\left(\frac{3}{2}\right)^2} \\
|AP|=\sqrt{\frac{9}{4}+\frac{9}{4}} \\
|AP|=\sqrt{\frac{18}{4}} \\
|AP|=\sqrt{\frac{9}{2}} \\
|AP|=\frac{\sqrt{9}}{\sqrt{2}} \\
|AP|=\frac{3}{\sqrt{2}} \\
|AP|=\frac{3\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
|AP|=\frac{3\sqrt{2}}{2}$$
Długość odcinka \(AP\) przyda nam się tak naprawdę tylko do tego, aby wyznaczyć długość odcinka \(AB\). Symetralna dzieli bok na dwie równe części, zatem odcinek \(AB\) będzie dwukrotnie dłuższy od odcinka \(AP\), czyli:
$$|AB|=2\cdot|AP| \\
|AB|=2\cdot\frac{3\sqrt{2}}{2} \\
|AB|=3\sqrt{2}$$
Krok 6. Obliczenie długości odcinka \(CP\).
Odcinek \(CP\) jest wysokością naszego trójkąta, czyli miarą którą potrzebujemy do obliczenia pola powierzchni trójkąta. Znamy współrzędne punktu \(C\) oraz \(P\), zatem:
$$|CP|=\sqrt{(x_{P}-x_{C})^2+(y_{P}-y_{C})^2} \\
|CP|=\sqrt{\left(-5-\left(-\frac{5}{2}\right)\right)^2+\left(5-\frac{5}{2}\right)^2} \\
|CP|=\sqrt{\left(-5+\frac{5}{2}\right)^2+\left(5-\frac{5}{2}\right)^2} \\
|CP|=\sqrt{\left(-\frac{5}{2}\right)^2+\left(\frac{5}{2}\right)^2} \\
|CP|=\sqrt{\frac{25}{4}+\frac{25}{4}} \\
|CP|=\sqrt{\frac{50}{4}} \\
|CP|=\frac{\sqrt{50}}{\sqrt{4}} \\
|CP|=\frac{\sqrt{25\cdot2}}{2} \\
|CP|=\frac{5\sqrt{2}}{2}$$
Krok 7. Obliczenie pola trójkąta \(ABC\).
Znamy długość podstawy \(|AB|=3\sqrt{2}\), wiemy też że wysokość trójkąta jest równa \(|CP|=\frac{5\sqrt{2}}{2}\), zatem pole powierzchni tej figury będzie równe:
$$P=\frac{1}{2}\cdot|AB|\cdot|CP| \\
P=\frac{1}{2}\cdot3\sqrt{2}\cdot\frac{5\sqrt{2}}{2} \\
P=\frac{15\cdot2}{2\cdot2} \\
P=\frac{30}{4} \\
P=7\frac{1}{2}$$