Rozwiązanie
Krok 1. Obliczenie miejsc zerowych wielomianu.
Jak to w standardowej nierówności kwadratowej bywa - na początku musimy obliczyć miejsca zerowe. Nie musimy tutaj potęgować tego wyrażenia w nawiasie. Wyrażenie \((3x+9)^2\) będzie równe \(0\) tylko i wyłącznie wtedy, kiedy wartość w nawiasie będzie równa \(0\). Zatem:
$$3x+9=0 \\
3x=-9 \\
x=-3$$
Krok 2. Szkicowanie wykresu paraboli.
Gdybyśmy wykonali potęgowanie, to przed \(x^2\) nie stałaby żadna wartość ujemna, zatem współczynnik kierunkowy \(a\) jest dodatni, a co za tym idzie, parabola będzie mieć ramiona skierowane do góry. Zaznaczamy na osi miejsce zerowe (kropka niezamalowana, bo w nierówności wystąpił znak \(\gt\)) i szkicujemy parabolę:
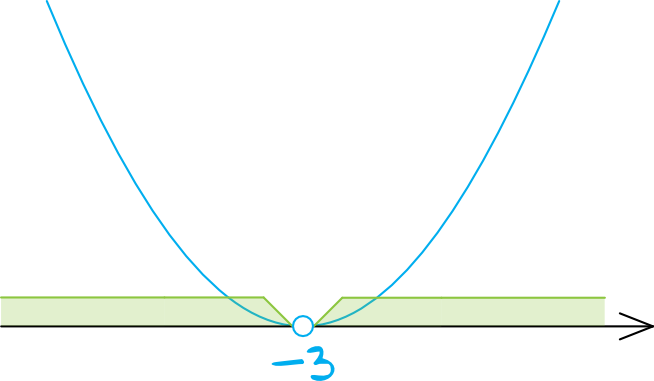
Krok 3. Odczytanie rozwiązania.
Interesują nas wartości większe od zera, czyli wszystko to, co znalazło się nad osią iksów. Widzimy wyraźnie, że w takim razie nierówność spełnia praktycznie każda liczba, oprócz \(-3\) (bo dla \(x=-3\) mamy wartość równą \(0\)). Dlatego też rozwiązaniem tej nierówności jest zbiór liczb rzeczywistych bez \(-3\).