Rozwiązanie
Krok 1. Wyznaczenie współrzędnych środka okręgu.
Równanie okręgu o środku w punkcie \(S=(a;b)\) oraz promieniu \(r\) przyjmuje postać:
$$(x-a)^2+(y-b)^2=r^2$$
Spróbujmy teraz dopasować równanie z treści zadania do powyższej postaci (czyli musimy doprowadzić do sytuacji w której w obydwu nawiasach mamy minusy):
$$(x-3)^2+(y+2)^2=r^2 \\
(x-3)^2+(y-(-2))^2=r^2$$
Teraz możemy bez przeszkód odczytać, że współrzędne środka okręgu to \(S=(3;-2)\).
Krok 2. Sporządzenie rysunku pomocniczego.
Narysujmy teraz okrąg o środku \(S=(3;-2)\), który jest styczny do osi igreków.
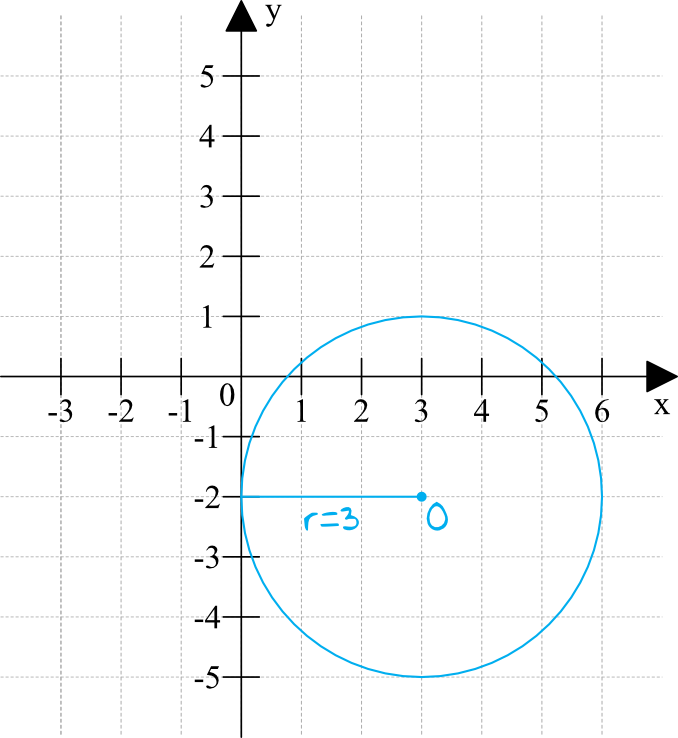
Krok 3. Odczytanie rozwiązania.
Z rysunku możemy wprost odczytać, że aby taki okrąg był styczny do osi igreków, to jego promień musi mieć długość \(r=3\).