Rozwiązanie
Krok 1. Obliczenie długości jednej z krawędzi prostopadłościanu.
Na razie potraktujmy to zadanie jako typowy przykład z ciągów. Z treści zadania możemy wywnioskować, że liczby \(a\), \(b\) oraz \(c\) tworzą ciąg geometryczny, a iloczyn tych liczb jest równy \(216\). Czyli mamy taką oto sytuację:
$$a\cdot b\cdot c=216$$
Z własności ciągów geometrycznych wiemy, że dla trzech kolejnych wyrazów ciągu geometrycznego zachodzi równość \({a_{2}}^2=a_{1}\cdot a_{3}\), czyli w naszym przypadku \(b^2=a\cdot c\). Skoro tak, to możemy podstawić tę zależność do naszego zapisu:
$$a\cdot b\cdot c=216 \\
a\cdot c\cdot b=216 \\
b^2\cdot b=216 \\
b^3=216 \\
b=6$$
Krok 2. Ustalenie, jakie są wymiary pozostałych boków.
Wiemy już, że jeden z boków ma długość \(b=6\). Tym samym możemy zapisać, że:
$$a\cdot6\cdot c=216 \\
a\cdot c=36$$
Z treści zadania wynika, że wszystkie długości krawędzi są liczbami naturalnymi. Musimy się więc zastanowić jakie dwie liczby naturalne pomnożone przez siebie dają wynik równy \(36\). Będą to:
$$1\cdot36=36 \\
2\cdot18=36 \\
3\cdot12=36 \\
4\cdot9=36 \\
6\cdot6=36$$
Możemy więc mówić o następujących ciągach:
I wersja: \(1,6,36 \Rightarrow q=6\)
II wersja \(2,6,18 \Rightarrow q=3\)
III wersja \(3,6,12 \Rightarrow q=2\)
IV wersja \(4,6,9 \Rightarrow q=1,5\)
V wersja \(6,6,6 \Rightarrow q=1\)
I, IV oraz V wersję musimy odrzucić, ponieważ iloraz ciągu ma być liczbą pierwszą, a zarówno \(1\), jak i \(1,5\) jak i \(6\) nie są takimi liczbami. To oznacza, że warunki naszego zadania spełniają dwa prostopadłościany: \(2\times6\times18\) oraz \(3\times6\times12\).
Krok 3. Obliczenie długości przekątnej prostopadłościanu.
Mamy dwa prostopadłościany spełniające warunki zadania, więc i dwie przekątne będziemy musieli obliczyć. Spójrzmy na rysunek pomocniczy:
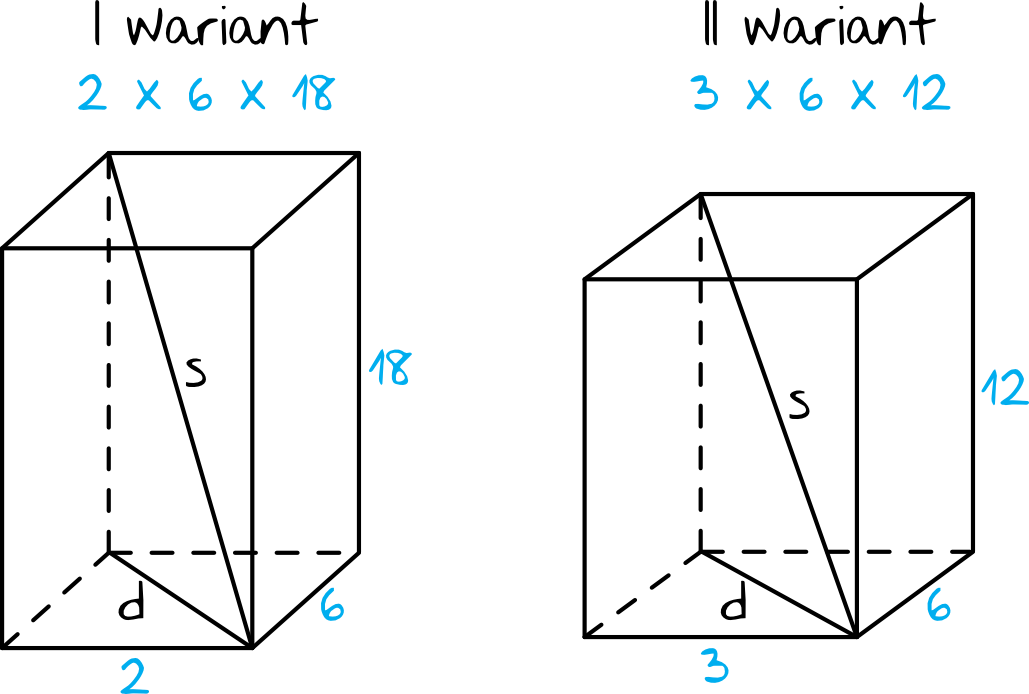
Do wyznaczenia długości przekątnej prostopadłościanu potrzebujemy znać długość przekątnej podstawy. Obliczmy zatem tę długość w pierwszym i drugim wariancie:
I wariant - \(2\times6\times18\)
$$2^2+6^2=d^2 \\
4+36=d^2 \\
d^2=40 \\
d=\sqrt{40} \quad\lor\quad d=-\sqrt{40}$$
Ujemny wynik odrzucamy, zatem zostaje nam \(d=\sqrt{40}\) (i póki co możemy to zostawić w takiej postaci).
II wariant - \(3\times6\times12\)
$$3^2+6^2=d^2 \\
9+36=d^2 \\
d^2=45 \\
d=\sqrt{45} \quad\lor\quad d=-\sqrt{45}$$
I tutaj także ujemny wynik odrzucamy, zatem zostaje nam \(d=\sqrt{45}\).
Teraz mając długości przekątnych podstawy, możemy obliczyć długości przekątnych całego prostopadłościanu:
I wariant - \(2\times6\times18\)
$$18^2+(\sqrt{40})^2=s^2 \\
324+40=s^2 \\
s^2=364 \\
s=\sqrt{364} \quad\lor\quad s=-\sqrt{364}$$
Ujemny wynik odrzucamy, zatem zostaje nam \(s=\sqrt{364}\), co możemy jeszcze rozpisać jako \(s=\sqrt{4\cdot91}=2\sqrt{91}\)
II wariant - \(3\times6\times12\)
$$12^2+(\sqrt{45})^2=s^2 \\
144+45=s^2 \\
s^2=189 \\
s=\sqrt{189} \quad\lor\quad s=-\sqrt{189}$$
Ujemny wynik odrzucamy, zatem zostaje nam \(s=\sqrt{189}\), co możemy jeszcze rozpisać jako \(s=\sqrt{9\cdot21}=3\sqrt{21}\).