Rozwiązanie
Krok 1. Sporządzenie rysunku wykresu funkcji.
Podana w zadaniu funkcja jest tak naprawdę funkcją wykładniczą \(2^x\), która jest przesunięta o \(3\) jednostki w dół. Musimy więc narysować najpierw naszą funkcję wykładniczą, a następnie wykonać jej przesunięcie. Aby narysować wykres funkcji wykładniczej \(2^x\) dobrze jest obliczyć i zaznaczyć najbardziej charakterystyczne punkty przez które taki wykres przechodzi. Z racji tego iż jest to zadanie otwarte, to powinniśmy wykonać ten wykres dość szczegółowo, stąd też policzymy sobie kilka takich kluczowych miejsc:
Dla \(x=0\) funkcja \(2^x\) przyjmuje wartość \(2^0=1\)
Dla \(x=1\) funkcja \(2^x\) przyjmuje wartość \(2^1=2\)
Dla \(x=2\) funkcja \(2^x\) przyjmuje wartość \(2^2=4\)
Dla \(x=-1\) funkcja \(2^x\) przyjmuje wartość \(2^{-1}=\frac{1}{2}\)
Dla \(x=-2\) funkcja \(2^x\) przyjmuje wartość \(2^{-2}=\frac{1}{4}\)
Teraz możemy narysować wykres funkcji \(2^x\) (linia niebieska), a następnie przesunąć każdy z punktów o trzy jednostki w dół otrzymując wykres funkcji \(2^x-3\) (linia zielona).
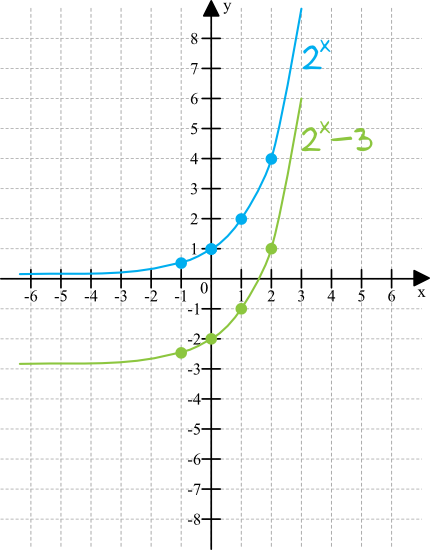
Krok 2. Odczytanie zbioru wartości funkcji.
Zbiór wartości odczytujemy z osi igreków. Widzimy wyraźnie, że nasza zielona funkcja zbliża się do \(y=-3\), ale nigdy tej linii nie osiągnie. To oznacza, że zbiorem wartości funkcji \(f(x)=2^x-3\) jest y\in(-3;+\infty).