Na rysunku przedstawiono wykres funkcji \(f\).

Funkcja \(h\) określona jest dla \(x\in\langle-3,5\rangle\) wzorem \(h(x)=f(x)+q\), gdzie \(q\) jest pewną liczbą rzeczywistą. Wiemy, że jednym z miejsc zerowych funkcji \(h\) jest liczba \(x_{0}=-1\).
a) Wyznacz \(q\).
b) Podaj wszystkie pozostałe miejsca zerowe funkcji \(h\).
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Narysujmy sobie jak musi wyglądać nasza funkcja \(h(x)\) wiedząc, że jest ona przesuniętą postacią funkcji \(f(x)\) w taki sposób, że miejscem zerowym tej funkcji jest teraz \(x=-1\).
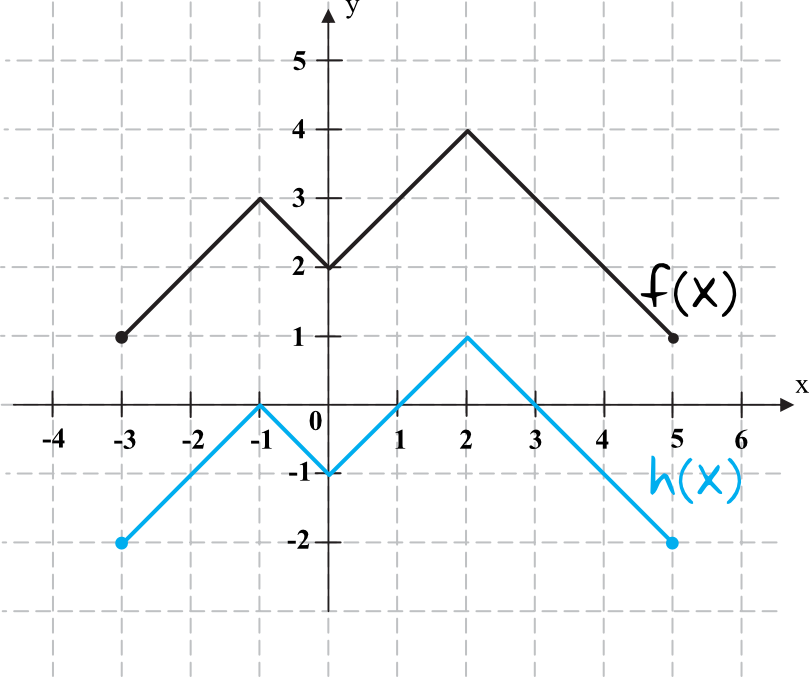
Krok 2. Określenie wartości \(q\).
Wykres funkcji \(h(x)\) trzeba było przesunąć o trzy jednostki do dołu, zatem:
$$h(x)=f(x)+q \\
h(x)=f(x)-3 \\
\text{zatem:} q=-3$$
Krok 3. Odczytanie wszystkich miejsc zerowych.
Z rysunku możemy odczytać pozostałe miejsca zerowe tej funkcji. Oprócz \(x=-1\) miejscami zerowymi są także \(x=1\) oraz \(x=3\).
Odpowiedź:
a) \(q=-3\)
b) \(x=1\) oraz \(x=3\)

