Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego ABC: A=(-3;-3) i C=(2;7) oraz prosta

Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego \(ABC\): \(A=(-3;-3)\) i \(C=(2;7)\) oraz prosta o równaniu \(y=\frac{3}{4}x-\frac{3}{4}\), zawierająca przeciwprostokątną \(AB\) tego trójkąta.

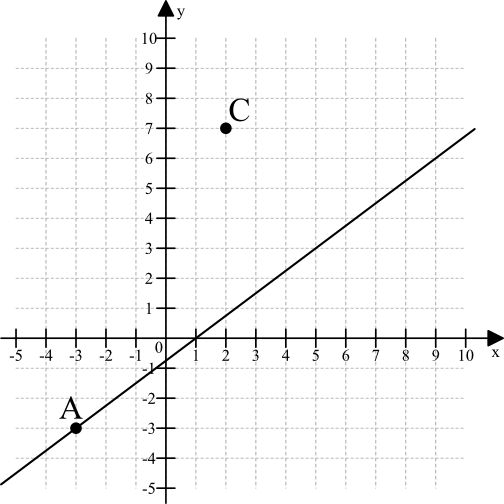
Oblicz współrzędne wierzchołka \(B\) tego trójkąta i długość odcinka \(AB\).

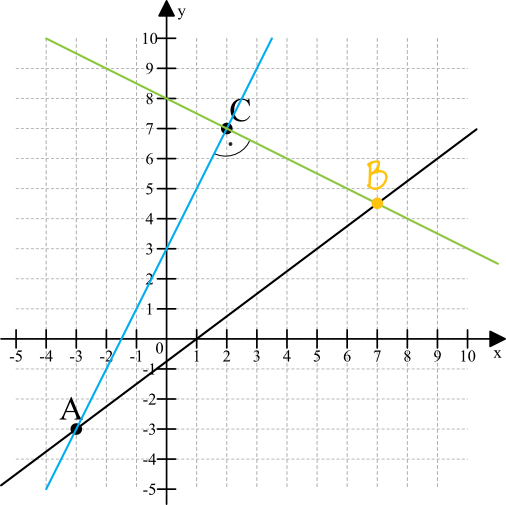
Do zadania możemy podejść tak naprawdę na dwa sposoby. Pierwszy sposób polegałby na tym, że wyznaczylibyśmy sobie równanie prostej przechodzącej przez punkty \(AC\), a następnie wyznaczylibyśmy równanie prostej prostopadłej (czyli poznalibyśmy wzór prostej \(BC\)). Znając wzór prostej \(BC\) łatwo wyznaczylibyśmy współrzędne punktu \(B\), bo to będzie punkt przecięcia się prostej \(BC\) oraz prostej której wzór jest podany w treści zadania. To jest taki standardowy sposób rozwiązywania tego typu zadań.

My jednak policzymy sobie to nieco sprytniej i zastosujemy tutaj drugi sposób, który wykorzystuje Twierdzenie Pitagorasa.

Do wyznaczenia współrzędnych punktu \(B\) wykorzystamy wzór na długość odcinka w układzie współrzędnych:
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2}$$

Analogicznie możemy wyznaczyć w ten sposób długości odcinków \(AC\) czy też \(BC\).

Współrzędne punktów \(A\) i \(C\) są nam znane, więc możemy w prosty sposób wyznaczyć długość odcinka \(AC\). Bez znajomości współrzędnych punktu \(B\) nie będziemy w stanie obliczyć natomiast długości odcinków \(AB\) oraz \(BC\), ale przy wykorzystaniu Twierdzenia Pitagorasa będziemy w stanie utworzyć równanie, które pozwoli nam wyznaczyć współrzędne punktu \(B\). Dla przejrzystości obliczeń przyjmijmy, że współrzędne punktu \(B\) to \(x\) oraz \(y\):
$$\require{cancel}
|BC|^2+|AC|^2=|AB|^2 \\
(x-2)^2+(y-7)^2+(2-(-3))^2+(7-(-3))^2=(x-(-3))^2+(y-(-3))^2 \\
(x-2)^2+(y-7)^2+5^2+10^2=(x+3)^2+(y+3)^2 \\
\cancel{x^2}-4x+4+\cancel{y^2}-14y+49+25+100=\cancel{x^2}+6x+9+\cancel{y^2}+6y+9 \\
-4x-14y+178=6x+6y+18 \\
10x+20y=160 \quad\bigg/:10 \\
x+2y=16$$

Tak na marginesie to otrzymaliśmy w ten sposób równanie prostej \(BC\). Gdybyśmy chcieli, to moglibyśmy je jeszcze przekształcić i zapisać w postaci kierunkowej, czyli \(y=-\frac{1}{2}x+8\).

Wracając do otrzymanego równania \(x+2y=16\), to teraz pod wartość \(y\) możemy podstawić równanie prostej na której leży nasz punkt \(B\), czyli \(y=\frac{3}{4}x-\frac{3}{4}\) i otrzymamy:
$$x+2\cdot\left(\frac{3}{4}x-\frac{3}{4}\right)=16 \\
x+\frac{6}{4}x-\frac{6}{4}=16 \quad\bigg/\cdot4 \\
4x+6x-6=64 \\
10x=70 \\
x=7$$

Podstawiając teraz wartość tej współrzędnej do równania prostej z treści zadania wyznaczymy także wartość współrzędnej \(y\):
$$y=\frac{3}{4}\cdot7-\frac{3}{4} \\
y=\frac{21}{4}-\frac{3}{4} \\
y=\frac{18}{4}=4\frac{1}{2}$$

Otrzymaliśmy w ten sposób współrzędne \(B=(7;4\frac{1}{2})\).

Znając współrzędne punktów \(A\) i \(B\) obliczymy długość odcinka \(AB\) z wykorzystaniem wzoru o którym mówiliśmy sobie w drugim kroku:
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2} \\
|AB|=\sqrt{\left(7-(-3)\right)^2+\left(4\frac{1}{2}-(-3)\right)^2} \\
|AB|=\sqrt{10^2+7\frac{1}{2}^2} \\
|AB|=\sqrt{100+\left(\frac{15}{2}\right)^2} \\
|AB|=\sqrt{\frac{400}{4}+\frac{225}{4}} \\
|AB|=\sqrt{\frac{625}{4}} \\
|AB|=\frac{25}{2}=12\frac{1}{2}$$

\(B=(7;4\frac{1}{2})\) oraz \(|AB|=12\frac{1}{2}\)