Ułamki zwykłe i dziesiętne - zadania (egzamin ósmoklasisty)
Zadanie 4. (1pkt) Ile spośród liczb: \(\frac{2}{3}, \frac{1}{2}, \frac{10}{25}, \frac{1}{4}\) spełnia warunek \(\frac{2}{5}\lt x\lt\frac{3}{5}\)?
Wyjaśnienie:
Aby wskazać które liczby spełniają ten warunek musimy albo wszystkie ułamki sprowadzić do wspólnego mianownika, albo zamienić te wszystkie ułamki na ułamki dziesiętne. Wygodniej będzie chyba wykonać zamianę na ułamki dziesiętne:
$$\frac{2}{3}\approx0,67 \\
\frac{1}{2}=0,5 \\
\frac{10}{25}=0,4 \\
\frac{1}{4}=0,25$$
Oraz ułamki z naszego warunku:
$$\frac{2}{5}=0,4 \\
\frac{3}{5}=0,6$$
Szukamy więc ułamków które są większe niż \(0,4\) i mniejsze niż \(0,6\). To oznacza, że tylko jeden ułamek spełnia warunki zadania i jest to ułamek \(\frac{1}{2}\).
Zadanie 8. (1pkt) Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami \(\bbox[5px,border:1px solid]{A}\) i \(\bbox[5px,border:1px solid]{B}\) oraz odpowiedź spośród oznaczonych literami \(\bbox[5px,border:1px solid]{C}\) i \(\bbox[5px,border:1px solid]{D}\).
Wartość wyrażenia \(4,5:0,75\) jest równa wartości wyrażenia \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\).
Wartość wyrażenia \(1,25\cdot0,4\) jest równa wartości wyrażenia \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\).
Wyjaśnienie:
Krok 1. Rozwiązanie pierwszej części zadania.
$$4,5:0,75=\frac{4,5}{0,75}=\frac{4,5\cdot100}{0,75\cdot100}=\frac{450}{75}$$
Krok 2. Rozwiązanie drugiej części zadania.
$$1,25\cdot0,4=\frac{1,25\cdot100}{100}\cdot\frac{0,4\cdot10}{10}=\frac{125}{100}\cdot\frac{4}{10}=\frac{125\cdot4}{1000}$$
Zadanie 10. (1pkt) Dane są trzy wyrażenia arytmetyczne:
I. \(75,5\cdot2-7\cdot6,99\)
II. \((4,6+5,5)\cdot10\)
III. \(0,26\cdot400\)
Które spośród tych wyrażeń mają wartość większą od \(100\)?
Wyjaśnienie:
Obliczmy po kolei wartość każdego z podanych wyrażeń:
I. \(75,5\cdot2-7\cdot6,99=151-48,93=102,07\)
II. \((4,6+5,5)\cdot10=10,1\cdot10=101\)
III. \(0,26\cdot400=104\)
Widzimy, że wszystkie wyrażenia mają wartość większą od \(100\).
Zadanie 13. (1pkt) Zaokrąglenie ułamka okresowego \(9,2(6)\) z dokładnością do \(0,001\) jest równe:
Wyjaśnienie:
$$9,2(6)=9,26666...$$
Na czwartym miejscu po przecinku rozpisanego ułamka okresowego znajduje się szóstka, więc będziemy zaokrąglać do góry. Skoro tak to:
$$9,2666\approx9,267$$
Zadanie 16. (1pkt) Do trzech jednakowych naczyń wlano tyle wody, że w pierwszym naczyniu woda zajmowała \(\frac{2}{3}\) pojemności, w drugim: \(\frac{3}{4}\) pojemności, a w trzecim \(\frac{5}{7}\) pojemności danego naczynia.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
W naczyniu drugim było mniej wody niż w naczyniu trzecim.
W pierwszym i drugim naczyniu łącznie było tyle samo wody, co w trzecim naczyniu.
Odpowiedź
1) FAŁSZ
2) FAŁSZ
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Aby ocenić prawdziwość tego zdania musimy porównać do siebie dwa ułamki - \(\frac{3}{4}\) oraz \(\frac{5}{7}\). Sprowadzając te ułamki do wspólnego mianownika otrzymamy:
II naczynie: \(\frac{3}{4}=\frac{21}{28}\)
III naczynie: \(\frac{5}{7}=\frac{20}{28}\)
To oznacza, że w drugim naczyniu było więcej wody niż w trzecim, czyli zdanie jest fałszem.
Krok 2. Ocena prawdziwości drugiego zdania.
W pierwszym i drugim naczyniu mamy:
$$\frac{2}{3}+\frac{3}{4}=\frac{8}{12}+\frac{9}{12}=\frac{17}{12}=1\frac{5}{12}$$
W trzecim naczyniu mamy raptem \(\frac{5}{7}\) pojemności, czyli znacznie mniej niż w pierwszym i drugim naczyniu łącznie. Zdanie jest więc fałszem.
Zadanie 17. (1pkt) Energię zużywaną przez organizm człowieka można wyrażać w kilokaloriach (kcal) lub w kilodżulach (kJ). Przyjmij, że \(1\) kcal=\(4,19\) kJ. Wskaż prawidłową odpowiedź.
Wyjaśnienie:
Sprawdźmy poprawność każdej z proponowanych odpowiedzi:
Odp. A. \(130\) kcal to \(54,47\) kJ
Obliczenie: \(130kcal=130\cdot4,19=544,7kJ\)
Odp. B. \(5447\) kcal to \(130\) kJ
Obliczenie: \(5447kcal\cdot4,19=22822,93kJ\)
Odp. C. \(130\) kcal to \(544,7\) kJ
Obliczenie: \(130kcal=130\cdot4,19=544,7kJ\)
Odp. D. \(544,7\) kcal to \(130\) kJ
Obliczenie: \(544,7kcal\cdot4,19=2282,293kJ\)
Prawidłowe przeliczenie znalazło się więc w trzeciej odpowiedzi.
Zadanie 18. (2pkt) Paweł powiedział, że podzieli tabliczkę czekolady w taki sposób, że bratu przypadnie \(\frac{1}{2}\) całej tabliczki, siostrze \(\frac{5}{12}\) całej tabliczki, a jemu \(\frac{1}{6}\) całej tabliczki. Czy taki podział tabliczki czekolady jest możliwy? Uzasadnij swoją odpowiedź.
Odpowiedź
Nie, ponieważ Paweł rozdzielił łącznie \(1\frac{1}{12}\) czekolady.
Wyjaśnienie:
Zsumujmy wszystkie ułamki, zgodnie z tym jak Paweł chciał podzielić czekoladę:
$$\frac{1}{2}+\frac{5}{12}+\frac{1}{6}=\frac{6}{12}+\frac{5}{12}+\frac{2}{12}=\frac{13}{12}=1\frac{1}{12}$$
Okazuje się, że zaproponowany podział jest niemożliwy, ponieważ suma wszystkich udziałów jest większa od \(1\). Można więc powiedzieć, że Paweł rozdzielił więcej czekolady, niż miał do dyspozycji.
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy otrzymany wynik jest błędny w wyniku błędu rachunkowego.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 19. (2pkt) Śniadanie Michała:
\(200g\) bułki paryskiej
\(30g\) masła śmietankowego
\(50g\) sera edamskiego tłustego
\(40g\) szynki wieprzowej gotowanej
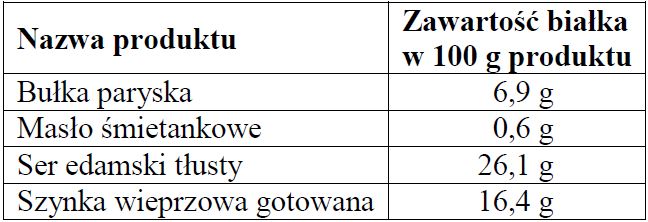
Oblicz masę białka zawartego w śniadaniu Michała.
Odpowiedź
Masa białka wynosi \(33,59g\).
Wyjaśnienie:
Krok 1. Obliczenie ilości białka w każdym z produktów.
Tabela zawartości białka zawiera informację o tym ile jest białka w \(100g\) produktu. Musimy więc obliczyć ile gramów białka znajduje się w poszczególnych produktach, uwzględniając ich wagę. Najprościej będzie to zrobić za pomocą proporcji:
Bułka:
Skoro \(100g\) bułki to \(6,9g\) białka
Więc \(200g\) bułki to \(13,8g\) białka
Masło:
Skoro \(100g\) masła to \(0,6g\) białka
To \(10g\) masła to \(0,06g\) białka
Więc \(30g\) masła to \(0,18g\) białka
Ser:
Skoro \(100g\) sera to \(26,1g\) białka
To \(50g\) sera to \(13,05g\) białka
Szynka:
Skoro \(100g\) szynki to \(16,4g\) białka
To \(10g\) szynki to \(1,64g\) białka
Więc \(40g\) szynki to \(6,56g\) białka
Krok 2. Obliczenie łącznej zawartości białka.
Znając już zawartość białka w każdym z produktów możemy bez problemu dodać do siebie te wyniki i w ten sposób zakończyć całe zadanie:
$$13,8g+0,18g+13,05g+6,56g=33,59g$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz ilość białka w każdym z produktów (Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Bardzo pomocne polecam
Również polecam
super zadania
Moim zdaniem parę zadań mogłoby być trudniejszych, lecz to nie zmienia faktu, że zadania są świetne i naprawdę polecam.
przydatne, polecam
Bardzo super!!
Polecam!
Polecam serdecznie!
Pozdrawiam wszystkich ósmoklasistów powodzenia Kochani.
Fajne zadania
fajne zadania
powodzenia na egzaminach
zadania są trudne ale wyjaśnienia nawet pomocne
Autor ma zamiłowanie do odpowiedzi B i C hahha
super dzięki polecam
mega przydatne polecam
Bardzo fajne zadania
super ćwiczenia, ale przydało by się te nieco starsze powyrzucać i dać bardziej aktualne.
Ale „stare” zadania są równie dobre i przydatne jak te „nowe” :)