Rozwiązanie
Krok 1. Obliczenie miary kąta \(ABC\).
W równoległoboku kąty przy jednym ramieniu mają łączną miarę \(180°\). Skoro tak, to kąt \(ABC\) ma miarę:
$$180°-106°=74°$$
Krok 2. Obliczenie miary kąta \(AED\).
Skoro kąt \(ABC\) ma miarę \(74°\), to kąt \(ADE\) ma także miarę \(74°\). Wiemy, że trójkąt \(ADE\) jest równoramienny, zatem kąty przy jego podstawie muszą mieć tą samą miarę. Skoro tak, to kąt \(DAE\) jest również kątem o mierze \(74°\). Powstała nam więc następująca sytuacja:
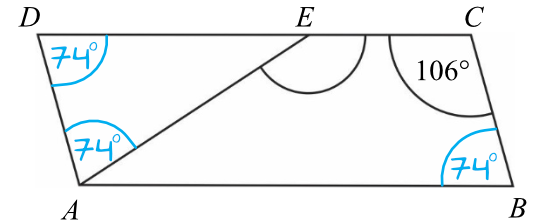
Teraz spójrzmy na trójkąt \(ADE\). Znamy miary dwóch kątów w tym trójkącie, zatem bez przeszkód obliczymy miarę tego trzeciego kąta:
$$|\sphericalangle AED|=180°-74°-74°=32°$$
Krok 3. Obliczenie miary kąta \(AEC\).
Kąty \(AED\) oraz \(AEC\) to kąty przyległe, a więc ich łączna miara wynosi \(180°\). Znając miarę kąta \(AED\) możemy zapisać, że:
$$|\sphericalangle AEC|=180°-32°=148°$$