Rozwiązanie
Krok 1. Wyznaczenie współrzędnych środka okręgu oraz długości promienia.
Równanie okręgu o środku w punkcie \(S=(a;b)\) oraz promieniu \(r\) przyjmuje postać:
$$(x-a)^2+(y-b)^2=r^2$$
Musimy więc przekształcić nasze równanie z treści zadania do takiej właśnie postaci jak powyżej, dzięki czemu błyskawicznie odczytamy współrzędne środka okręgu oraz długość jego promienia. Zrobimy to w następujący sposób:
$$(x-1)^2+y^2=4 \\
(x-1)^2+(y-0)^2=2^2$$
Z tak zapisanego równania możemy odczytać, że \(S=(1;0)\) oraz \(r=2\).
Krok 2. Sporządzenie rysunku pomocniczego.
Narysujmy teraz nasz okręg oraz prostą \(y=-1\) i sprawdźmy ile mają punktów wspólnych:
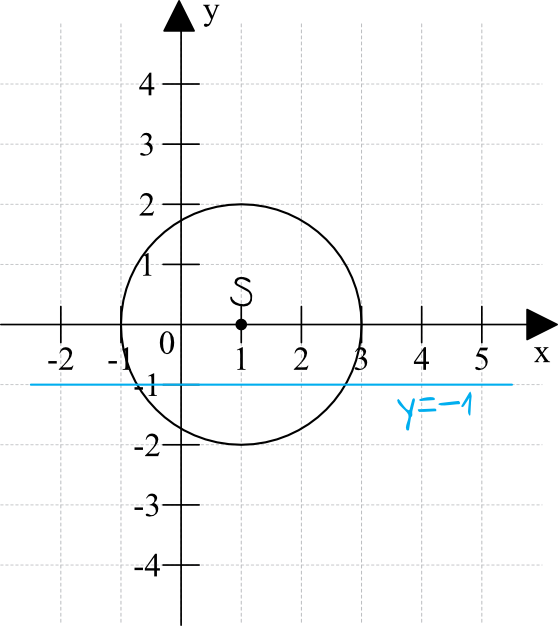
Z rysunku wynika dość jasno, że okrąg ma dwa wspólne punkty z prostą.