Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy sobie ten ostrosłup i zaznaczmy w nim najistotniejsze długości które potem przydadzą nam się do obliczenia pożądanych wartości.
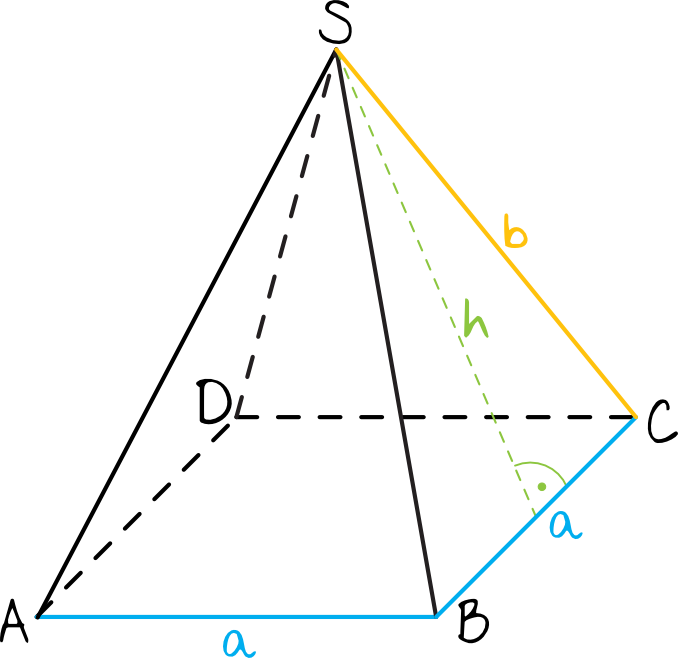
Krok 2. Obliczenie pola podstawy.
Skoro pole powierzchni całkowitej wynosi \(144cm^2\) z czego pole powierzchni bocznej jest równe \(80cm^2\), to znaczy że pole podstawy jest równe:
$$144cm^2-80cm^2=64cm^2$$
Krok 3. Obliczenie krawędzi podstawy.
Z treści zadania wiemy, że jest to ostrosłup prawidłowy czworokątny, a skoro tak, to w jego podstawie znajduje się kwadrat. My o tym kwadracie wiemy już to, że jego pole powierzchni jest równe \(64cm^2\), zatem krawędź tego kwadratu ma długość:
$$P=a^2 \\
64cm^2=a^2 \\
a=8cm$$
Krok 4. Obliczenie wysokości ściany bocznej.
Spróbujmy teraz obliczyć wysokość trójkąta znajdującego się w ścianie bocznej ostrosłupa. Wiemy, że pole powierzchni bocznej jest równe \(80cm^2\), a skoro powierzchnię boczną tworzą cztery jednakowe trójkąty, to każdy z nich ma pole powierzchni równe:
$$80cm^2:4=20cm^2$$
Wiemy więc, że trójkąt będący ścianą boczną ma długość podstawy \(a=8cm\), wiemy też że jego pole powierzchni jest równe \(20cm^2\), więc bez przeszkód obliczymy wysokość tego trójkąta.
$$P=\frac{1}{2}ah \\
20cm^2=\frac{1}{2}\cdot8cm\cdot h \\
20cm^2=4cm\cdot h \\
h=5cm$$
Krok 5. Obliczenie długości krawędzi bocznej ostrosłupa.
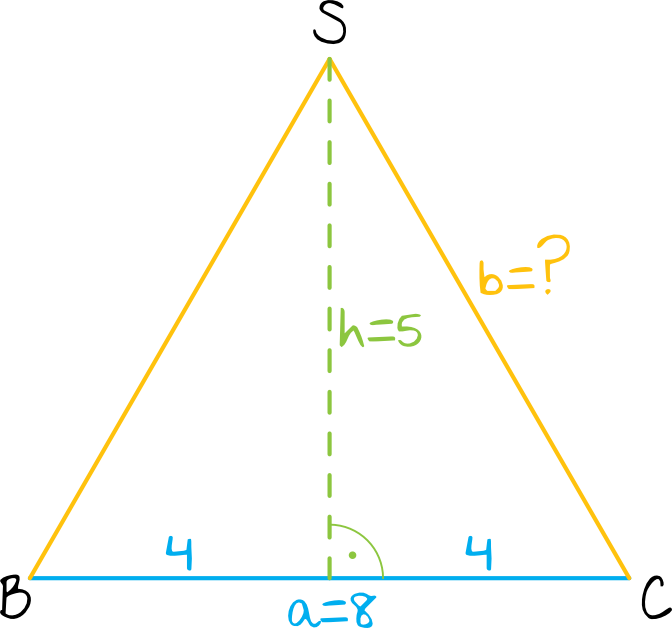
W ścianach bocznych naszego ostrosłupa znajdują się trójkąty równoramienne, więc wysokość podzieliła nam podstawę na dwie równe części. To pozwala nam na obliczenie długości krawędzi bocznej (czyli długości \(b\)) za pomocą Twierdzenia Pitagorasa:
$$4^2+5^2=b^2 \\
16+25=b^2 \\
b^2=41 \\
b=\sqrt{41}[cm]$$