Krótszy bok prostokąta ma długość \(6\). Kąt między przekątną prostokąta i dłuższym bokiem ma miarę \(30°\). Dłuższy bok prostokąta ma długość:
\(2\sqrt{3}\)
\(4\sqrt{3}\)
\(6\sqrt{3}\)
\(12\)
Rozwiązanie:
Krok 1. Obliczenie długości boku prostokąta.
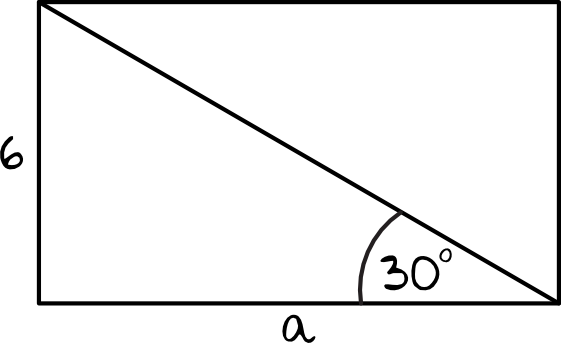
Skorzystamy z funkcji trygonometrycznych, a dokładniej z tangensa:
$$tg30°=\frac{6}{a} \\
\frac{\sqrt{3}}{3}=\frac{6}{a} \\
\frac{\sqrt{3}}{3}a=6 \quad\bigg/\cdot\frac{3}{\sqrt{3}} \\
a=\frac{18}{\sqrt{3}}$$
Krok 2. Usunięcie niewymierności z mianownika.
Obliczona przed chwilą długość jest poprawna, ale nie mamy takiej odpowiedzi w proponowanych. Musimy więc jeszcze usunąć niewymierność z mianownika, mnożąc licznik i mianownik przez \(\sqrt{3}\):
$$a=\frac{18\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \\
a=\frac{18\sqrt{3}}{3} \\
a=6\sqrt{3}$$
Odpowiedź:
C. \(6\sqrt{3}\)


hej! Czy można to zadanie obliczyć za pomocą własności trójkąta 90,30,60?
Witaj! Jak najbardziej można ;)