Rozwiąż nierówność \(8x^2-72x\le0\).
Rozwiązanie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Oczywiście tę nierówność można obliczyć metodą delty, pamiętając tylko o tym, że w tym przypadku \(c=0\). Istnieje jednak znacznie prostsza metoda na wyznaczenie miejsc zerowych. Przyrównujemy wielomian do zera i zapisujemy go w postaci iloczynowej:
$$8x^2-72x=0 \\
8x(x-9)=0 \\
8x=0 \quad\lor\quad x-9=0 \\
x=0 \quad\lor\quad x=9$$
Krok 2. Szkicowanie wykresu paraboli.
Ramiona paraboli będą skierowane do góry, bo współczynnik \(a=8\) (czyli jest dodatni). Zaznaczamy na osi wyznaczone przed chwilą miejsca zerowe, pamiętając o tym że kropki będą zamalowane (bo w nierówności wystąpił znak \(\le\)).
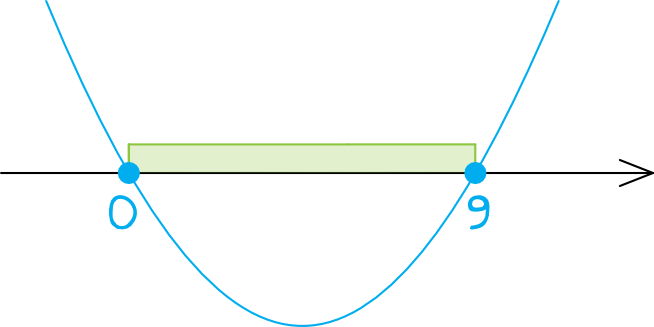
Krok 3. Odczytanie rozwiązania.
Interesują nas wartości mniejsze lub równe zero, zatem poprawnym rozwiązaniem tej nierówności będzie przedział \(x\in\langle0;9\rangle\).
Odpowiedź:
\(x\in\langle0;9\rangle\)

