Rozwiązywanie nierówności kwadratowych ma wiele wspólnego z rozwiązywaniem równań kwadratowych. Aby więc łatwiej było zrozumieć to zagadnienie zachęcam Cię do zapoznania się z tym jak rozwiązujemy równania kwadratowe (o ile jeszcze tego nie umiesz):
Zacznijmy naukę od prostego przykładu:
Na początku rozwiązywania nierówności musimy ją potraktować tak, jakby to było równanie kwadratowe, czyli musimy rozwiązać równanie \(2x^2+3x-2=0\). Po co to robimy, skoro w nierówności nie ma znaku \(=\), tylko jest \(\lt\)? Robimy to, ponieważ chcemy się dowiedzieć kiedy wyrażenie \(2x^2+3x-2\) jest równe \(0\). Ta informacja przyda nam się do zaznaczenia miejsc zerowych wykresu paraboli z której potem odczytamy ostateczne rozwiązanie nierówności.
Pierwszym naszym krokiem jest więc rozwiązanie równania \(2x^2+3x-2=0\) i tu właśnie przyda nam się znajomość rozwiązywania równań kwadratowych. Jeśli pamiętamy ten dział, to wiemy że w tym przypadku równanie zapisane jest w postaci ogólnej, czyli takiej z której możemy obliczyć deltę. Wypiszmy zatem najpierw współczynniki (odczytując bezpośrednio jakie liczby znalazły się przed \(x^2\), przed \(x\) oraz w wyrazie wolnym):
Współczynniki: \(a=2,\;b=3,\;c=-2\)
Współczynniki mamy odczytane, zatem możemy przejść do obliczenia delty:
$$Δ=b^2-4ac \\
Δ=3^2-4\cdot2\cdot(-2) \\
Δ=9-(-16)=9+16=25$$
Wiemy już, że \(Δ=25\), więc zgodnie z zasadami rozwiązywania równań kwadratowych musimy obliczyć pierwiastek z delty:
$$\sqrt{Δ}=\sqrt{25}=5$$
Teraz możemy przystąpić do wyznaczenia rozwiązań naszego równania:
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-3-5}{2\cdot2}=\frac{-8}{4}=-2 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-3+5}{2\cdot2}=\frac{2}{4}=\frac{1}{2}$$
W przypadku równań kwadratowych otrzymane wyniki \(x=-2\) oraz \(x=\frac{1}{2}\) byłyby już naszymi ostatecznymi rozwiązaniami. W nierównościach musimy jeszcze wykonać jeden krok, a mianowicie naszkicować wykres paraboli określonej wzorem \(2x^2+3x-2\). Wiemy, że miejscami zerowymi tej paraboli są wyznaczone przed chwilą \(x=-2\) oraz \(x=\frac{1}{2}\), zatem mamy dwie możliwości jak taka parabola może wyglądać:
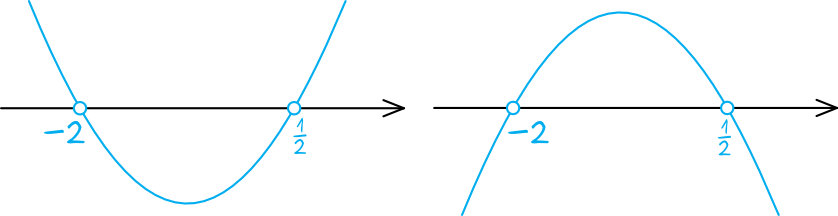
Jak się dowiedzieć, która z tych możliwości jest poprawna? O tym, czy ramiona paraboli są skierowane do góry czy do dołu decyduje współczynnik \(a\), który odczytujemy z postaci ogólnej (czyli jest to liczba znajdująca się przed \(x^2\)). Jeżeli współczynnik \(a\) jest dodatni, to parabola będzie mieć ramiona skierowane do góry. Jeżeli współczynnik \(a\) jest ujemny, to parabola będzie mieć ramiona skierowane do dołu. W naszym przypadku \(a=2\), czyli jest to wartość dodatnia. W związku z tym poprawnym wykresem paraboli będzie:
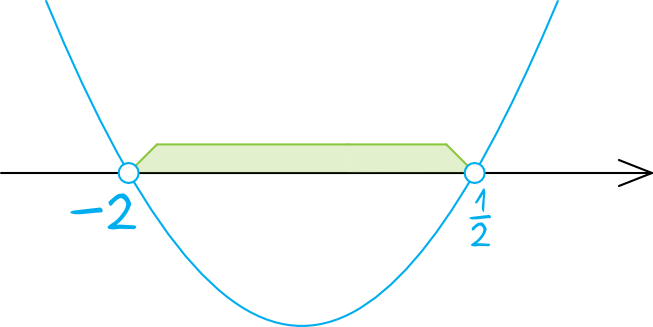
Teraz musimy już odczytać rozwiązania naszej nierówności. Szukamy wartości dla których wyrażenie \(2x^2+3x-2\) przyjmuje wartości mniejsze od zera. Wartości mniejsze od zera to te, które znajdują się pod osią. Z wykresu możemy odczytać, że wartości mniejsze od zera są przyjmowane dla przedziału liczb od \(-2\) do \(\frac{1}{2}\) i taka też będzie nasza odpowiedź. Rozwiązaniem nierówności będzie zatem przedział: \(x\in(-2;\frac{1}{2})\).
Z pierwszej nierówności płynie dla nas następujący wniosek, że rozwiązanie nierówności kwadratowej odbywa się w następujący sposób:
1. Przenosimy wyrazy na lewą stronę (o ile coś jest po prawej stronie) i rozwiązujemy nierówność tak jakby to było równanie kwadratowe, wyznaczając w ten sposób miejsca zerowe.
2. Szkicujemy parabolę zaznaczając obliczone miejsca zerowe i określając przy tym czy parabola ma ramiona skierowane do góry (\(a\gt0\)), czy do dołu (\(a\lt0\)).
3. Odczytujemy z rysunku rozwiązanie nierówności, które zazwyczaj będzie przedziałem lub sumą przedziałów.
Cała więc trudność tkwi w umiejętnym rozwiązywaniu równań kwadratowych, dzięki której wyznaczamy miejsca zerowe paraboli. Jeżeli to potrafimy wykonywać, to i samo rozwiązywanie nierówności nie powinno nam sprawiać problemów.
Powyższa nierówność jest niemalże identyczna co poprzednia, z tą tylko różnicą że tutaj mamy \(\gt\), a tam mieliśmy \(\lt\). Co się zmieni w naszych obliczeniach? Tak naprawdę to nie zmieni się praktycznie nic – delta jest ta sama, \(x_{1}\) oraz \(x_{2}\) są takie same, zatem i rysunek będzie identyczny. To co będzie inne, to sam odczyt rozwiązania. Żeby więc nie powtarzać obliczeń to od razu przejdźmy do rysunku paraboli:
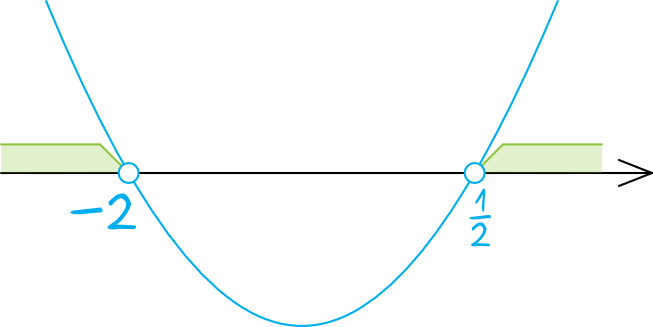
Tym razem interesuje nas sytuacja w której wartości są większe od zera, czyli te które znajdują się nad osią. Widzimy wyraźnie, że są dwie części wykresu, które musimy uwzględnić: od minus nieskończoności do \(-2\) oraz od \(\frac{1}{2}\) do plus nieskończoności. W związku z tym rozwiązaniem tej nierówności będzie suma przedziałów: \(x\in(-\infty;-2)\cup(\frac{1}{2};+\infty)\)
Ponownie mamy identyczną nierówność, ale tym razem mamy znak \(\ge\). Co się zmieni w całym toku rozwiązywania względem poprzedniego przykładu? Zmieni się jedynie to, że tym razem z wykresu paraboli chcemy odczytać nie tylko to co jest nad osią, ale także to co jest na osi. W takich sytuacjach kiedy mamy w nierówności znaki \(\ge\) oraz \(\le\) bardzo często symbolicznie zamalowujemy kropki znajdujące się przy miejscach zerowych, tak aby pokazać, że one także są uwzględniane w rozwiązaniu:
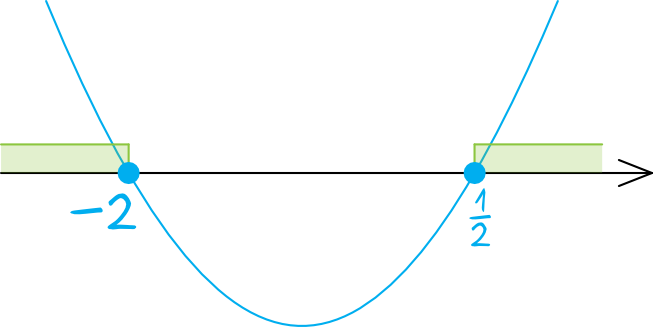
Sam zapis sumy przedziałów będzie niemal identyczny, z tą tylko różnicą, że przy \(-2\) oraz \(\frac{1}{2}\) będziemy mieć tym razem nawiasy domknięte (ostre). Rozwiązaniem tej nierówności będzie zatem: $$x\in(-\infty;-2\rangle\cup\left\langle\frac{1}{2};+\infty\right)$$
Tym razem mamy zupełnie nowe liczby, zatem będziemy musieli wykonać tu pewne obliczenia. Jednak zanim zaczniemy cokolwiek liczyć, to musimy przenieść wszystkie wartości na lewą stronę (dokładnie tak jak to miało miejsce w przypadku równań kwadratowych). Robimy to po to, by móc za chwilę rozwiązać równanie kwadratowe korzystając z delty.
$$-x^2+5x\gt6 \\
-x^2+5x-6\gt0$$
Teraz możemy przystąpić do obliczeń, a zaczniemy tradycyjnie od wyznaczenia miejsc zerowych. Przyrównując \(-x^2+5x-6\) do zera otrzymamy równanie \(-x^2+5x-6=0\), czyli:
Współczynniki: \(a=-1,\;b=5,\;c=-6\)
$$Δ=b^2-4ac \\
Δ=5^2-4\cdot(-1)\cdot(-6) \\
Δ=25-24=1$$
$$\sqrt{Δ}=\sqrt{1}=1$$
Znając pierwiastek z delty, możemy przejść do obliczenia rozwiązań równania:
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-5-1}{2\cdot(-1)}=\frac{-6}{-2}=3 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-5+1}{2\cdot(-1)}=\frac{-4}{-2}=2$$
Teraz szkicujemy wykres paraboli nanosząc na oś wyznaczone przed chwilą miejsca zerowe \(x=2\) oraz \(x=3\). Ustalmy jeszcze jaki jest kierunek ramion paraboli? Skoro współczynnik \(a=-1\) (czyli jest ujemny), to ramiona paraboli będą tym razem skierowane do dołu. Całość zatem będzie wyglądać w następujący sposób:

Teraz musimy odczytać rozwiązania z naszego rysunku. Interesują nas wartości większe od zera, a te są przyjmowane w przedziale \(x\in(2;3)\).
Aby rozpocząć obliczanie nierówności musimy wyznaczyć miejsca zerowe, czyli rozwiązać równanie \(x^2-9=0\). Możemy oczywiście tutaj liczyć deltę, pamiętając że w tym przypadku współczynnik \(b=0\). Jednak jest to równanie, które jesteśmy w stanie obliczyć w pamięci, przenosząc dziewiątkę na prawą stronę:
$$x^2-9=0 \\
x^2=9 \\
x=3 \lor x=-3$$
Czas więc na szkic paraboli. Znamy już miejsca zerowe, współczynnik \(a\) jest dodatni (konkretnie to \(a=1\), bo przed \(x^2\) nie stoi żadna wartość), czyli ramiona paraboli będą skierowane do góry. Parabola będzie więc wyglądać w ten oto sposób:
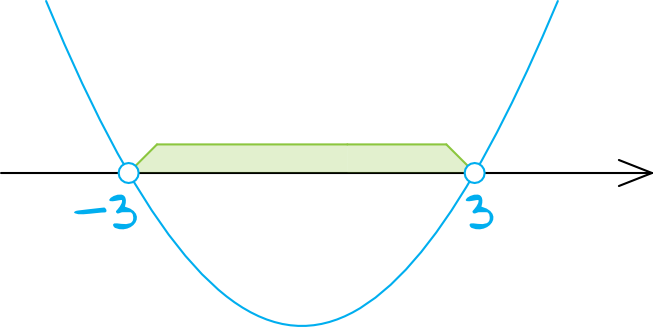
Na koniec musimy odczytać rozwiązania. Interesuje nas to co znalazło się pod osią iksów, bo szukamy wartości mniejszych od zera, zatem rozwiązaniem nierówności będzie przedział \(x\in(-3;3)\).
Takich różnych nierówności możemy wymyślać całą masę, a procedura liczenia jest cały czas taka sama i opiera się przede wszystkim na poprawnym rozwiązaniu równania kwadratowego. Spójrzmy na sam koniec na dwa problematyczne przypadki:
Zaczynamy od wyznaczenia miejsc zerowych, czyli rozwiązania równania \((x-5)(x+3)=0\). Sytuacja w tym zadaniu jest idealna, bo mamy tak zwaną postać iloczynową z której w prosty sposób wyznaczymy miejsca zerowe. Aby całość była równa zero, to jeden z nawiasów musi być równy zero, zatem:
$$x-5=0 \quad\lor\quad x+3=0 \\
x=5 \quad\lor\quad x=-3$$
Mamy więc już obliczone miejsca zerowe, czyli możemy przejść do rysowania paraboli. No i tu się pojawia kluczowe pytanie – jaki jest współczynnik \(a\)? W postaci ogólnej współczynnik \(a\) to była liczba stojąca przed \(x^2\), a tutaj? Powinniśmy pamiętać, że równania w postaci iloczynowej zapisujemy jako \(a(x-x_{1})(x-x_{2})=0\), zatem współczynnikiem \(a\) jest liczba stojąca przed nawiasami. W naszym przypadku przed nawiasami nie stoi nic, czyli to tak jakbyśmy mieli postać \(1\cdot(x-5)(x+3)\). Z tego też względu \(a=1\), czyli współczynnik jest dodatni.
Nie mniej jednak odczytywanie współczynnika \(a\) z postaci iloczynowej bywa zdradliwe, a to dlatego że czasem w nawiasach mamy nieco inną postać wyrażeń niż ta pożądana (np. możemy mieć \((-x-5)(2x+3)=0\), co tak do końca nie jest postacią iloczynową znaną nam z definicji). Dlatego też aby poznać wartość tego współczynnika możemy po prostu wymnożyć przez siebie te nawiasy, czyli doprowadzić równanie do postaci ogólnej. W naszej sytuacji byłoby to:
$$(x-5)(x+3)=x^2+3x-5x-15=x^2-2x-15$$
Teraz widzimy wyraźnie, że \(a=1\). Jak już nabierzemy wprawy przy rozwiązywaniu równań i nierówności, to zauważymy że nie musimy wymnażać wszystkich wyrazów, wystarczy wymnożyć te wyrazy z iksem, bo cała reszta nas nie interesuje.
Wracając do zadania – skoro więc współczynnik \(a\) jest dodatni, to parabola będzie mieć ramiona skierowane do góry:
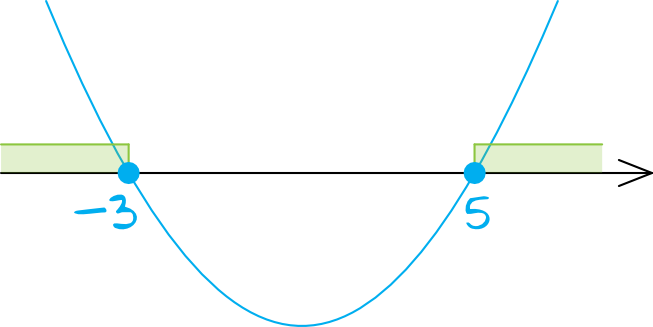
Interesują nas wartości większe od zera lub równe zero, czyli patrzymy na to co znajduje się nad osią oraz na osi. W związku z tym rozwiązaniem tej nierówności będzie przedział: \(x\in(-\infty;-3\rangle\cup\langle5;+\infty)\).
Na koniec omówimy sobie przykład, który sprawia bardzo dużo problemów i jest źródłem wielu nieporozumień. Zaczynamy od wyznaczenia miejsc zerowych, a skoro mamy postać ogólną, to zaczniemy od wypisania współczynników i obliczenia delty:
Współczynniki: \(a=2,\;b=-4,\;c=5\)
$$Δ=b^2-4ac \\
Δ=(-4)^2-4\cdot2\cdot7 \\
Δ=16-40=-24$$
Delta wyszła nam ujemna. Co to oznacza? Bardzo dużo osób twierdzi, że w związku z tym nierówność nie ma rozwiązań (bo tak przecież było w przypadku równań kwadratowych). To jest błędny wniosek. Ujemna delta oznacza, że \(2x^2-4x+5\) nigdy nie będzie równe \(0\), czyli po prostu nie mamy miejsc zerowych. Kwestia rozwiązań nierówności jest cały czas otwarta. Aby stwierdzić jakie jest dokładne rozwiązanie tej nierówności, musimy narysować parabolę, której ramiona są skierowane do góry (bo \(a=2\)) oraz która nie ma miejsc zerowych (czyli nie przecina nigdy osi iksów). W związku z tym szkic wyglądałby następująco:
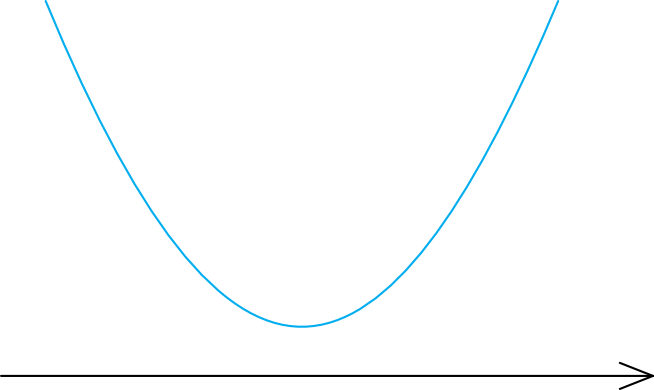
Teraz musimy z rysunku odczytać informację kiedy parabola przyjmuje wartości większe od zera. Okazuje się, że takie wartości są przyjmowane dla każdego iksa. To oznacza, że mimo ujemnej delty rozwiązaniem tej nierówności są wszystkie liczby rzeczywiste \(x\in\mathbb{R}\). Jakiejkolwiek liczby nie podstawimy pod iksa, to nasza nierówność będzie prawdziwa.

Dziękuje bardzo za pomoc