Krawędź sześcianu ma długość \(9\). Długość przekątnej tego sześcianu jest równa:
To zadanie jest bardzo proste jeśli pamiętamy że istnieje wzór na przekątną sześcianu. Sześcian o krawędzi \(a\) ma przekątną o długości \(a\sqrt{3}\). W związku z tym skoro w naszym zadaniu \(a=9\), to przekątna ma długość \(9\sqrt{3}\).
Tego wzoru niestety nie ma w tablicach maturalnych, dlatego też jeśli byśmy o nim nie pamiętali, to musimy obliczyć to zadanie na piechotę. Zróbmy sobie prosty rysunek pomocniczy:
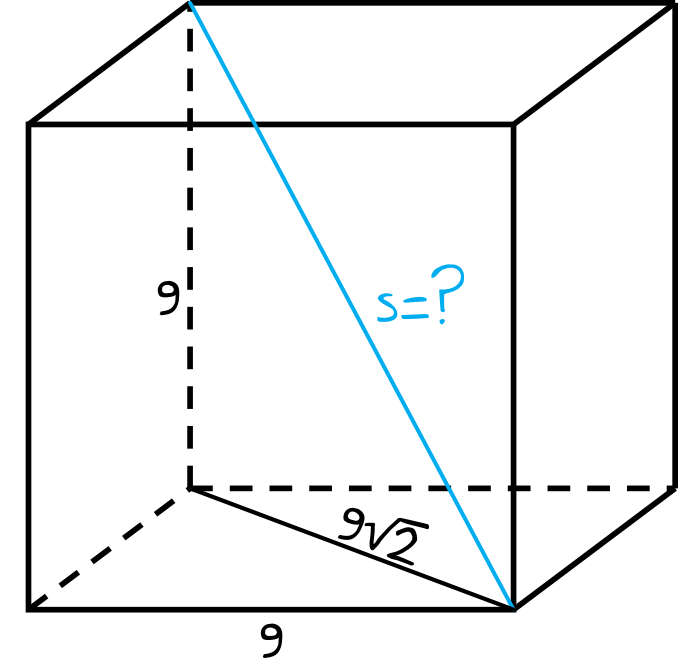
Przekątna kwadratu znajdującego się w podstawie ma długość \(a\sqrt{2}\), czyli w tym przypadku \(9\sqrt{2}\). Tworzy ona wraz z krawędzią boczną przyprostokątne trójkąta prostokątnego, w którym przeciwprostokątną jest nasza poszukiwana przekątna sześcianu. Korzystając więc z Twierdzenia Pitagorasa wyjdzie nam, że:
$$9^2+(9\sqrt{2})^2=s^2 \\
81+81\cdot2=s^2 \\
81+162=s^2 \\
s^2=243 \\
s=\sqrt{243}=\sqrt{81\cdot3}=9\sqrt{3}$$
C. \(9\sqrt{3}\)

