Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego i odczytanie wymiarów prostopadłościanu II.
Wiemy, że prostopadłościan I jest sześcianem, czyli wszystkie jego krawędzie muszą mieć jednakową długość. Skoro jedna z krawędzi ma długość \(3cm\), to znaczy że:
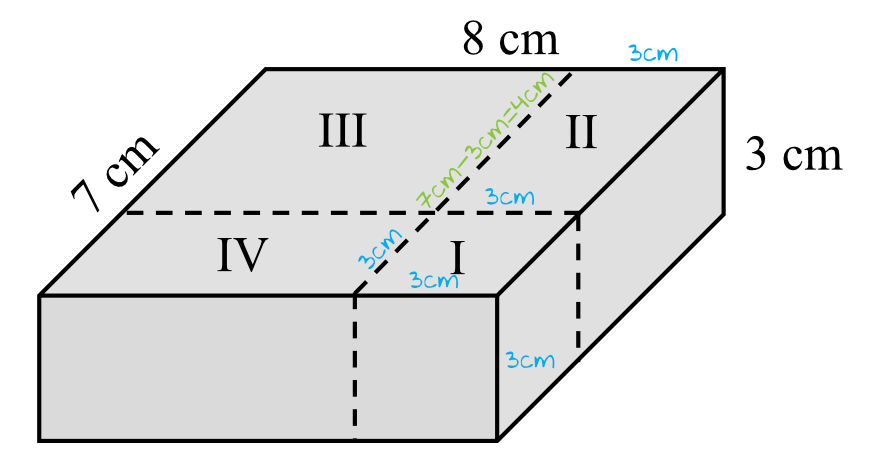
Ta prosta analiza pokazuje nam, że prostopadłościan II ma wymiary \(3cm\times4cm\times3cm\).
Krok 2. Obliczenie objętości prostopadłościanu II.
Korzystając ze wzoru na objętość prostopadłościanu możemy obliczyć, że:
$$V=abc \\
V=3cm\cdot4cm\cdot3cm \\
V=36cm^3$$