Objętość graniastosłupa

W tym temacie powiemy sobie jak obliczyć objętość graniastosłupa oraz rozwiążemy wspólnie kilka zadań związanych z objętością graniastosłupa.

Objętość graniastosłupa obliczamy ze wzoru:

$$V=P_{p}\cdot H$$
gdzie:
$V$ – objętość graniastosłupa
$P_{p}$ – pole podstawy graniastosłupa
$H$ – wysokość graniastosłupa

Bardzo często obliczając objętość nie będziemy liczyć oddzielnie pola powierzchni tylko po to, by potem podstawić tę wartość do wzoru. Z reguły wszystko będziemy zapisywać w jednym równaniu, bo tak jest zazwyczaj prościej i szybciej. Jeżeli więc przykładowo w podstawie graniastosłupa mamy np. kwadrat o boku $a$ i wiemy, że pole kwadratu obliczamy ze wzoru $P=a^2$, to często możemy spotkać się z sytuacją, że ktoś od razu zapisze, że w takim przypadku $V=a^2\cdot H$.

Przykład 1. Oblicz objętość poniższego graniastosłupa.

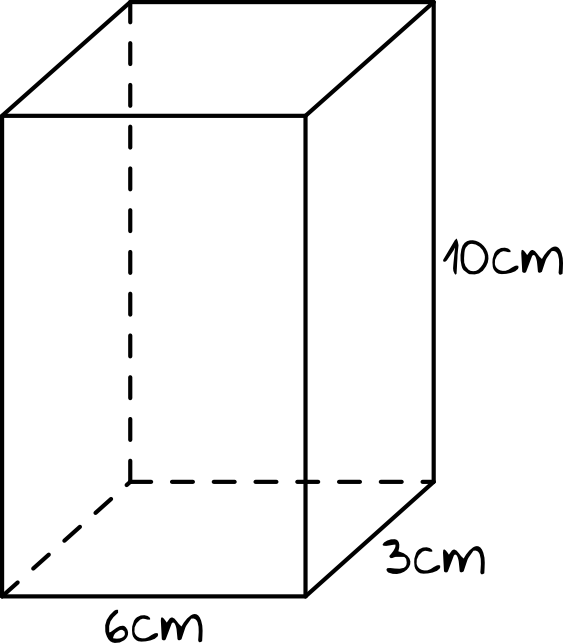
objętość graniastosłupa

Rozwiązanie:
W podstawie naszego graniastosłupa mamy prostokąt o wymiarach $6cm\times3cm$, a wysokość graniastosłupa ma długość $10cm$. Nie musimy liczyć oddzielnie pola powierzchni podstawy, możemy od razu zapisać, że:
$$V=P_{p}\cdot H \\
V=a\cdot b\cdot H \\
V=6cm\cdot3cm\cdot10cm \\
V=18cm^2\cdot10cm \\
V=180cm^3$$

Oczywiście jeżeli nie czujemy się pewnie na matematyce, to możemy najpierw obliczyć oddzielnie pole podstawy, a potem obliczyć objętość. Wtedy zapisalibyśmy, że:
$$P_{p}=a\cdot b \\
P_{p}=6cm\cdot3cm \\
P_{p}=18cm^2 \\

I teraz wiedząc, że $P_{p}=18cm^2$ oraz że $H=10cm$ moglibyśmy obliczyć objętość graniastosłupa:
$$V=P_{p}\cdot H \\
V=18cm^2\cdot10cm \\
V=180cm^2$$

Przykład 2. Oblicz objętość graniastosłupa prawidłowego trójkątnego, którego krawędź podstawy jest równa $6cm$, a wysokość jest równa $10cm$.

Rozwiązanie:
Tym razem zanim zaczniemy liczyć objętość to musimy w ogóle ustalić co tak naprawdę wynika z treści zadania. Mamy informację, że graniastosłup jest trójkątny, czyli w podstawie będzie miał trójkąt. Ale… to nie będzie byle jaki trójkąt. W treści zadania mamy podane, ze graniastosłup jest prawidłowy, a to z kolei oznacza, że w podstawie musimy mieć figurę foremną (czyli figurę, której wszystkie boki mają jednakową miarę). Wniosek z tego płynie taki, że w podstawie będziemy mieć trójkąt równoboczny, a skoro tak, to pole podstawy będziemy mogli obliczyć korzystając ze wzoru $P_{p}=\frac{a^2\sqrt{3}}{4}$.

I tutaj ponownie – możemy policzyć oddzielnie pole podstawy, a potem obliczymy objętość, albo też możemy od razu podstawić pod $P_{p}$ wzór na pole trójkąta równobocznego otrzymując postać:
$$V=\frac{a^2\sqrt{3}}{4}\cdot H$$

Znamy długość krawędzi podstawy $a=6cm$, znamy też wysokość całej bryły $H=10cm$, zatem:
$$V=\frac{6^2\sqrt{3}}{4}\cdot10 \\
V=\frac{36\sqrt{3}}{4}\cdot10 \\
V=9\sqrt{3}\cdot10 \\
V=90\sqrt{3} [cm^3]$$

Przykład 3. Oblicz wysokość graniastosłupa prawidłowego czworokątnego wiedząc, że $V=100cm^3$ oraz że krawędź podstawy ma długość $a=5cm$.

Rozwiązanie:
Tym razem wykorzystamy informację na temat objętości, aby obliczyć inną długość – w tym przypadku wysokość. Z treści zadania wynika, że graniastosłup jest prawidłowy, zatem wiemy już że w podstawie musi znaleźć się figura foremna. Tą figurą będzie tym razem kwadrat, bo graniastosłup jest czworokątny. Skoro znamy długość boku tego kwadratu i znamy objętość całej bryły, to okazuje się, że poszukiwana wysokość jest jedyną niewiadomą. Zatem:
$$V=P_{p}\cdot H \\
V=a^2\cdot H \\
100cm^3=(5cm)^2\cdot H \\
100cm^3=25cm^2\cdot H \\
H=4cm$$

Zobacz też: Objętość ostrosłupa

Zobacz też: Liczba ścian, krawędzi oraz wierzchołków graniastosłupa

Zobacz też: Pole powierzchni całkowitej graniastosłupa