Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
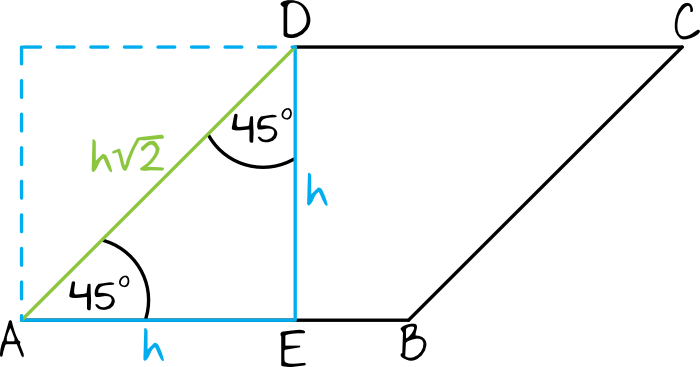
Spójrzmy na trójkąt \(AED\) który chcąc nie chcąc nam się tutaj stworzył. Jest to bardzo charakterystyczny trójkąt prostokątny \(45°,45°,90°\). Z własności tego trójkąta wynika, że jeżeli przyprostokątna ma długość \(h\), to przeciwprostokątna ma długość \(h\sqrt{2}\). Stąd też możemy zapisać, że:
$$|AD|=h\sqrt{2}$$
Krok 2. Obliczenie pola figury.
Skoro jest to romb, to wszystkie boki są równej długości. Stąd też także bok \(AB\) na który opuszczona jest wysokość będzie mieć długość \(a=h\sqrt{2}\). Znając długość podstawy możemy bez przeszkód obliczyć pole tego rombu:
$$P=a\cdot h \\
P=h\sqrt{2}\cdot h \\
P=h^2\sqrt{2}$$