Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają mieć jednakową długość, to powstanie nam taka oto bryła:
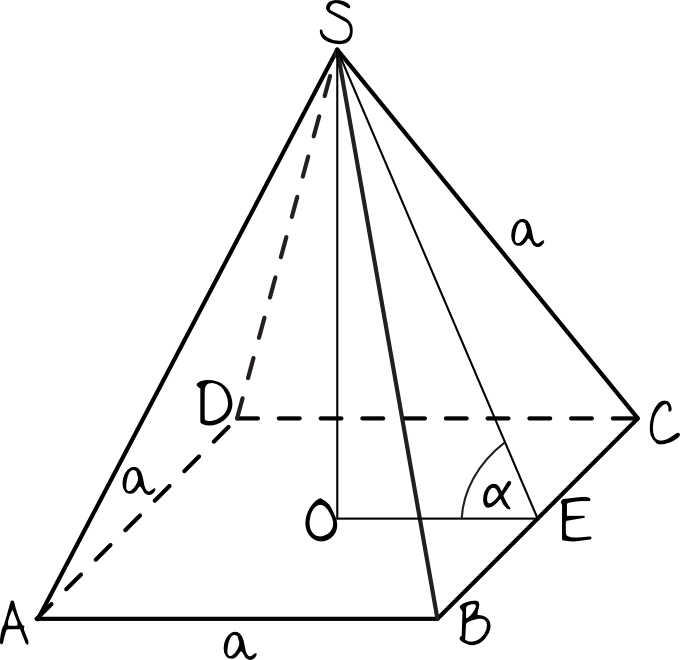
Krok 2. Zapisanie zależności kluczowych odcinków.
Spójrzmy teraz na nasz rysunek. Odcinek \(SE\) jest wysokością trójkąta równobocznego znajdującego się w ścianie bocznej. W związku z tym jego długość możemy zapisać jako:
$$|SE|=\frac{a\sqrt{3}}{2}$$
Teraz spójrzmy na odcinek \(OE\) - jest to połowa długości krawędzi bocznej, zatem:
$$|OE|=\frac{1}{2}a$$
Krok 3. Obliczenie długości odcinka \(SO\).
Do wyznaczenia sinusa kąta \(α\) potrzebna nam będzie znajomość długości odcinka \(SO\), a tą wyznaczymy z Twierdzenia Pitagorasa:
$$|OE|^2+|SO|^2=|SE|^2 \\
\left(\frac{1}{2}a\right)^2+|SO|^2=\left(\frac{a\sqrt{3}}{2}\right)^2 \\
\frac{a^2}{4}+|SO|^2=\frac{3a^2}{4} \\
|SO|^2=\frac{3a^2}{4}-\frac{a^2}{4} \\
|SO|^2=\frac{2a^2}{4} \\
|SO|=\frac{a\sqrt{2}}{2} \quad\lor\quad |SO|=-\frac{a\sqrt{2}}{2}$$
Wartość ujemną oczywiście pomijamy, bo bok nie może mieć ujemnej długości. Zostaje nam więc \(|SO|=\frac{a\sqrt{2}}{2}\).
Krok 4. Obliczenie wartości sinusa.
Teraz zgodnie z definicją sinusa możemy zapisać, że:
$$sinα=\frac{|SO|}{|SE|} \\
sinα=\frac{\frac{a\sqrt{2}}{2}}{\frac{a\sqrt{3}}{2}} \\
sinα=\frac{a\sqrt{2}}{2}:\frac{a\sqrt{3}}{2} \\
sinα=\frac{a\sqrt{2}}{2}\cdot\frac{2}{a\sqrt{3}} \\
sinα=\frac{\sqrt{2}}{\sqrt{3}} \\
sinα=\frac{\sqrt{2}\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \\
sinα=\frac{\sqrt{6}}{3}$$