Graniastosłup prawidłowy to graniastosłup, który w swojej podstawie ma figurę foremną, a wszystkie ściany boczne tej bryły są prostokątami prostopadłymi do podstawy. Dla przypomnienia – figura foremna to taka, której wszystkie boki i wszystkie kąty mają jednakową miarę. To oznacza, że w podstawie graniastosłupa prawidłowego może się znaleźć np. trójkąt równoboczny czy też kwadrat.
Figura znajdująca się w podstawie takiego graniastosłupa będzie też wpływać na pełną nazwę bryły. Przykładowo:
• graniastosłup prawidłowy trójkątny ma w swojej podstawie trójkąt równoboczny (nie może to być inny trójkąt).
• graniastosłup prawidłowy czworokątny ma w swojej podstawie kwadrat (nie może to być romb czy prostokąt, bo to nie są figury foremne).
• graniastosłup prawidłowy pięciokątny ma w swojej podstawie pięciokąt foremny.
Najbardziej charakterystycznym graniastosłupem prawidłowym jest sześcian, którego wszystkie ściany są kwadratami. Można więc powiedzieć, że sześcian jest szczególnym przypadkiem graniastosłupa prawidłowego czworokątnego.
Własności graniastosłupa prawidłowego
Graniastosłupy prawidłowe są bardzo częstymi bohaterami różnych zadań z bryłami, a to dlatego, że wiąże się z nimi szereg kluczowych własności, które wynikają wprost z figur foremnych znajdujących się w podstawie. Spójrzmy na dwa najbardziej charakterystyczne rysunki:
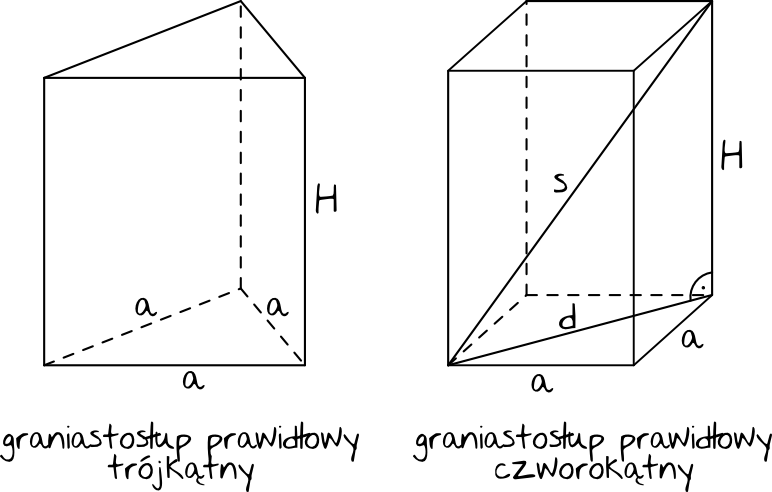
Na podstawie tych dwóch rysunków powiedzmy sobie o najważniejszych cechach, które mogą się przydać podczas rozwiązywania zadań:
Graniastosłup prawidłowy trójkątny:
• wiemy, że w podstawie jest trójkąt równoboczny. Z własności takich trójkątów wynika, że ich wysokość da się obliczyć ze wzoru \(h=\frac{a\sqrt{3}}{2}\), a pole da się obliczyć ze wzoru \(P=\frac{a^2\sqrt{3}}{4}\). To oznacza, że jak gdzieś w zadaniu mamy podaną długość krawędzi bocznej, to będziemy w stanie poznać wysokość lub pole trójkąta znajdującego się w podstawie i na odwrót – znając wysokość lub pole trójkąta będziemy w stanie poznać długość krawędzi podstawy.
• wszystkie ściany boczne mają jednakowe wymiary.
Graniastosłup prawidłowy czworokątny:
• w podstawie jest kwadrat, a z własności kwadratów wiemy, że przekątna kwadratu o boku \(a\) ma długość \(d=a\sqrt{2}\).
• podobnie jak w graniastosłupie prawidłowym trójkątnym, tak i tutaj wszystkie ściany boczne mają jednakowe wymiary.
• zwróć uwagę na to, że przekątna podstawy, wysokość graniastosłupa oraz przekątna całego graniastosłupa tworzą trójkąt prostokątny. To oznacza, że pewne miary będziemy mogli wyliczać czy to z Twierdzenia Pitagorasa, czy też z funkcji trygonometrycznych.
