Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zastanówmy się jak musi wyglądać wykres naszej funkcji. Skoro funkcja kwadratowa przyjmuje jakąś największą konkretną wartość, to całość musi wyglądać mniej więcej w ten sposób:
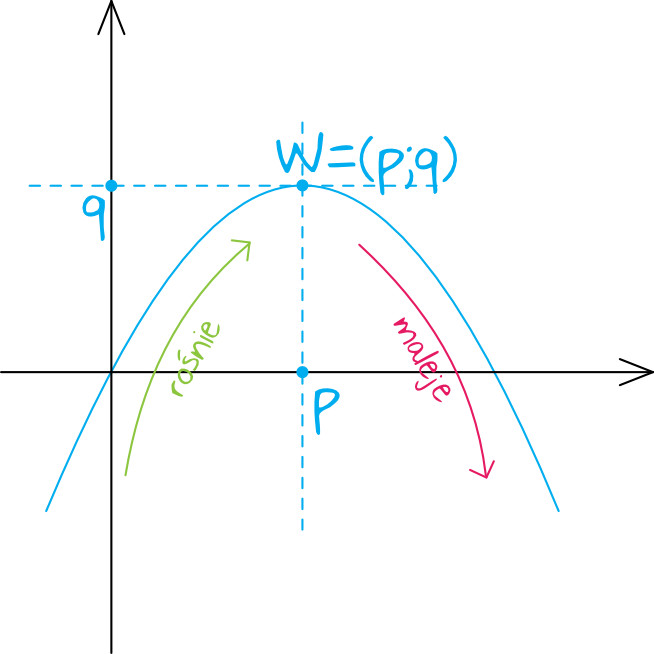
Skąd wiadomo, że ramiona tej paraboli będą skierowane do dołu? Gdyby skierowane były do góry, to ramiona sięgałyby nieskończoności, czyli funkcja miałaby wtedy nieskończenie wielką największą wartość dla nieskończenie wielkiego argumentu \(x\). Taka sytuacja nam nie odpowiada, bo wiemy że największa wartość osiągana jest dla \(x=2\). Nie ma więc innego wyjścia, funkcja musi mieć ramiona skierowane do dołu, wtedy swoją największą wartość osiągnie w wierzchołku paraboli.
Krok 2. Obliczenie wartości parametru \(m\).
Wiemy, że funkcja przyjmuje największą wartość dla \(x=2\), a to zgodnie z rysunkiem oznacza, że współrzędna iksowa wierzchołka paraboli (zapisywana jako \(p\)) jest równa \(2\). Czyli \(p=2\).
Ze wzorów z tablic możemy odczytać, że współrzędną \(p\) da się obliczyć korzystając ze wzoru \(p=\frac{-b}{2a}\) i to pozwoli nam wyznaczyć wartość parametru \(m\), który ukrył się we współczynniku \(a\). Zatem:
$$p=\frac{-b}{2a} \\
2=\frac{-16}{2\cdot(m+3)} \\
2=\frac{-16}{2m+6} \quad\bigg/\cdot(2m+6) \\
4m+12=-16 \\
4m=-28 \\
m=-7$$
Krok 3. Zapisanie wzoru funkcji.
Skoro \(m=-7\), to wzór naszej funkcji będzie następujący:
$$f(x)=(m+3)x^2+16x+5 \\
f(x)=(-7+3)x^2+16x+5 \\
f(x)=-4x^2+16x+5$$
Krok 4. Obliczenie największej wartości tej funkcji.
Wiemy, że największą wartość ta funkcja osiąga dla \(x=2\), zatem:
$$f(2)=-4\cdot2^2+16\cdot2+5 \\
f(2)=-4\cdot4+32+5 \\
f(2)=-16+32+5 \\
f(2)=16+5 \\
f(2)=21$$