Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
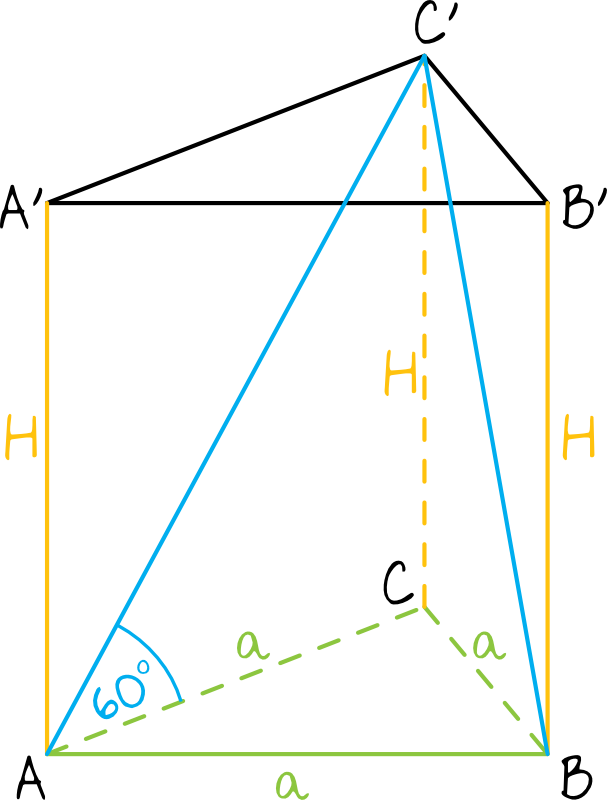
Krok 2. Zapisanie zależności między wysokością graniastosłupa i długością podstawy.
Spójrzmy na trójkąt \(ACC'\). Jest to na pewno trójkąt prostokątny w którym jak widzimy przyprostokątne mają długość \(a\) oraz \(H\). Korzystając z funkcji trygonometrycznych (a konkretnie z tangensa) możemy zapisać, że:
$$tg60°=\frac{H}{a} \\
\sqrt{3}=\frac{H}{a} \\
H=a\sqrt{3}$$
Krok 3. Obliczenie długości krawędzi podstawy.
Skorzystamy z informacji, która mówi nam, że ściana boczna będąca prostokątem o bokach \(a\) oraz \(H\) ma pole równe \(2\sqrt{3}\). Wiedząc, że \(H=a\sqrt{3}\) możemy zapisać, że:
$$P=a\cdot H \\
2\sqrt{3}=a\cdot a\sqrt{3} \\
2\sqrt{3}=a^2\sqrt{3} \quad\bigg/:\sqrt{3} \\
a^2=2 \\
a=\sqrt{2} \quad\lor\quad a=-\sqrt{2}$$
Ujemne rozwiązanie oczywiście odrzucamy, bo długość nie może być ujemna. Zostaje nam zatem \(a=\sqrt{2}\).
Krok 4. Obliczenie wysokości graniastosłupa.
Skoro \(a=\sqrt{2}\), a wiemy że \(H=a\sqrt{3}\), to znaczy że:
$$H=\sqrt{2}\cdot\sqrt{3} \\
H=\sqrt{6}$$
Krok 5. Obliczenie długości przekątnej ściany bocznej.
Skoro znamy długość \(a\) oraz \(H\) to jesteśmy w stanie obliczyć długość przekątnej ściany bocznej, czyli długość odcinka \(AC'\). Zrobimy to korzystając z Twierdzenia Pitagorasa:
$$(\sqrt{2})^2+(\sqrt{6})^2=|AC'|^2 \\
2+6=|AC'|^2 \\
|AC'|^2=8 \\
|AC'|=\sqrt{8} \quad\lor\quad |AC'|=-\sqrt{8}$$
Ujemne rozwiązanie odrzucamy, zatem zostaje nam \(|AC'|=\sqrt{8}\).
Krok 6. Obliczenie wysokości trójkąta \(ABC'\).
Dla przejrzystości obliczeń naszkicujmy sobie nasz kluczowy trójkąt \(ABC'\) i nanieśmy na niego dane, które obliczyliśmy w poprzednich krokach:
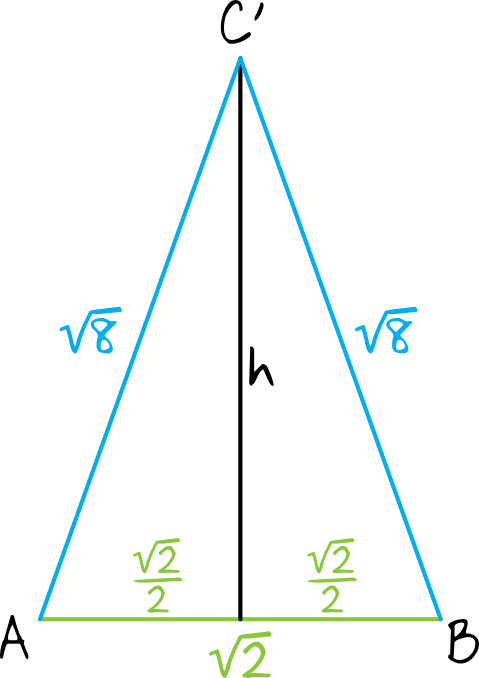
Teraz naszym zadaniem jest obliczenie pola powierzchni tego trójkąta, a aby to uczynić musimy poznać jeszcze jego wysokość. Widzimy, że to jest trójkąt równoramienny, dlatego mamy pewność że wysokość dzieli nam podstawę na dwie równe części. To pozwoli nam teraz obliczyć wysokość trójkąta korzystając z Twierdzenia Pitagorasa:
$$\left(\frac{\sqrt{2}}{2}\right)^2+h^2=(\sqrt{8})^2 \\
\frac{2}{4}+h^2=8 \\
h^2=\frac{15}{2} \\
h=\sqrt{\frac{15}{2}} \quad\lor\quad h=-\sqrt{\frac{15}{2}}$$
Ujemne rozwiązanie odrzucamy, bo wysokość musi być dodatnia. Zostaje nam zatem \(h=\sqrt{\frac{15}{2}}\).
Krok 7. Obliczenie pola trójkąta \(ABC'\).
Mamy już komplet danych, bowiem wiemy że podstawa trójkąta \(ABC'\) ma długość \(a=\sqrt{2}\), wiemy też że \(h=\sqrt{\frac{15}{2}}\), zatem:
$$P=\frac{1}{2}\cdot a\cdot h \\
P=\frac{1}{2}\cdot\sqrt{2}\cdot\sqrt{\frac{15}{2}} \\
P=\frac{1}{2}\cdot\sqrt{2}\cdot\frac{\sqrt{15}}{\sqrt{2}} \\
P=\frac{\sqrt{15}}{2}$$