Rozwiązanie
Krok 1. Zapisanie nierówności w postaci ogólnej.
Zanim zaczniemy liczyć, musimy przekształcić zapis nierówności. Będziemy dążyć do postaci ogólnej, zatem wszystkie wyrazy musimy przenieść na lewą stronę i poprawnie wymnożyć nawias:
$$x(2x-1)+4\gt8x \\
x(2x-1)+4-8x\gt0 \\
2x^2-x+4-8x\gt0 \\
2x^2-9x+4\gt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Teraz możemy przystąpić do obliczenia miejsc zerowych.
Współczynniki: \(a=2,\;b=-9,\;c=4\)
$$Δ=b^2-4ac=(-9)^2-4\cdot2\cdot4=81-32=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-9)-7}{2\cdot2}=\frac{9-7}{4}=\frac{2}{4}=\frac{1}{2} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-9)+7}{2\cdot2}=\frac{9+7}{4}=\frac{16}{4}=4$$
Krok 3. Szkicowanie wykresu paraboli.
Zaznaczamy otrzymane wyniki na osi liczbowej i rysujemy parabolę. Ramiona paraboli będą skierowane do góry, bo współczynnik \(a\) jest dodatni, zatem:
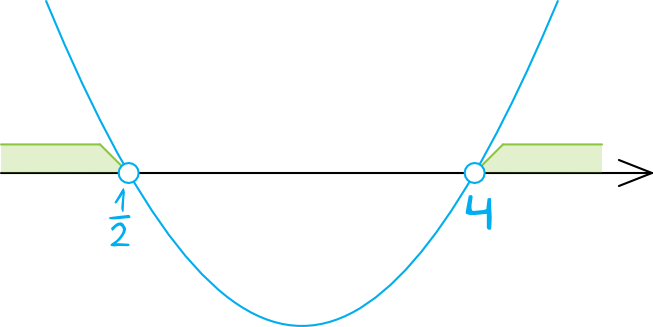
Krok 4. Odczytanie rozwiązania.
Interesują nas miejsca w których funkcja przyjmuje wartości większe zera. Patrzymy się zatem co znajduje się nad osią i widzimy, że rozwiązaniem tej nierówności będzie suma przedziałów \(x\in(-\infty;\frac{1}{2})\cup(4;+\infty)\)