Dany jest okrąg o środku w punkcie \(O\). Prosta \(KL\) jest styczna do tego okręgu w punkcie \(L\), a środek \(O\) tego okręgu leży na odcinku \(KM\) (zobacz rysunek). Udowodnij, że kąt \(KML\) ma miarę \(31°\).
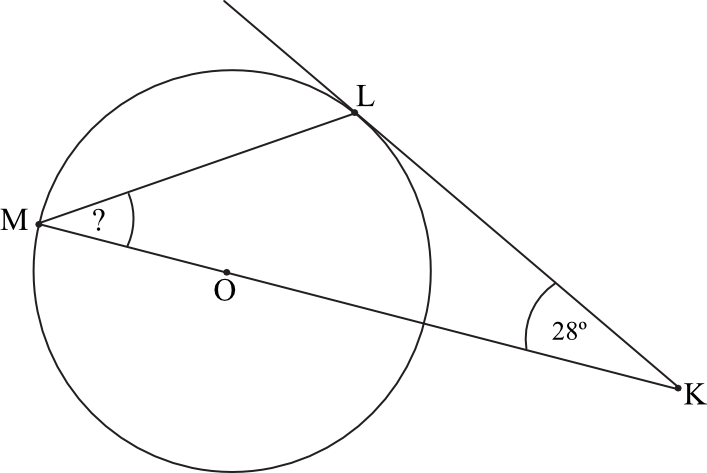
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Połączmy ze sobą punkty \(L\) oraz \(O\) (będzie to promień okręgu) i wprowadźmy sobie proste oznaczenia kątów:
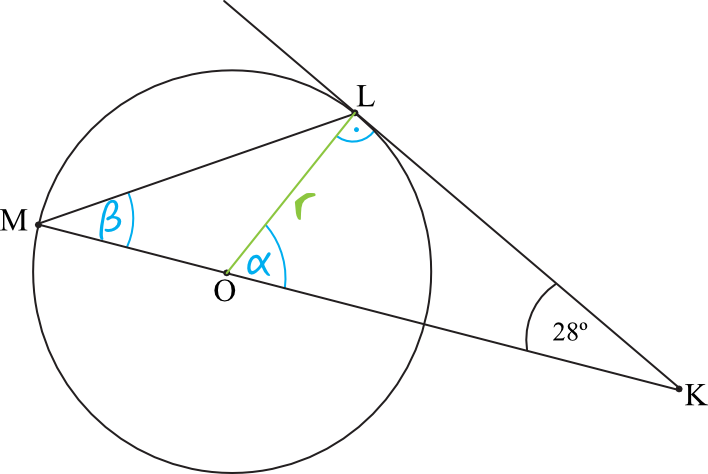
Z własności stycznych wiemy, że kąt między styczną, a promieniem okręgu, jest kątem prostym (patrz rysunek). To pozwoli nam w prosty sposób wyznaczyć miarę kąta \(α\).
Krok 2. Obliczenie miary kąta \(α\).
Skoro suma kątów w trójkącie \(OKL\) ma być równa \(180°\), to kąt \(α\) ma miarę:
$$α=180°-90°-28°=62°$$
Krok 3. Obliczenie miary kąta \(β\).
Z własności kątów środkowych i wpisanych opartych na tym samym łuku wiemy, że kąt wpisany w okręg (a takim jest nasz kąt \(β\)) jest dwa razy mniejszy od kąta środkowego (a takim jest tutaj kąt \(α\)). Zatem:
$$β=62°:2=31°$$
I właśnie to należało udowodnić.
Odpowiedź:
Udowodniono wykorzystując własności stycznej do okręgu.

