Funkcja liniowa określana jest wzorem \(f(x)=ax+b\), gdzie \(a\) i \(b\) są współczynnikami funkcji. Współczynnik \(a\) nazywamy też potocznie współczynnikiem kierunkowym, bo jak się za chwilę okaże, będzie od odpowiadał za kierunek biegu wykresu funkcji liniowej.
Przykładowymi wzorami funkcji liniowej będą:
$$f(x)=2x+3 \\
f(x)=-3x-\frac{1}{2} \\
f(x)=x-1$$
We wzorach funkcji (nie tylko liniowych) bardzo często zamiast \(f(x)=…\) możemy się spotkać z zapisem \(y=…\) np. \(y=2x+3\) lub \(y=-3x-\frac{1}{2}\). Jedna i druga forma zapisu znaczą dokładnie to samo.
Wykresem funkcji liniowej jest (jak sama nazwa wskazuje) linia prosta. Przykładowo:
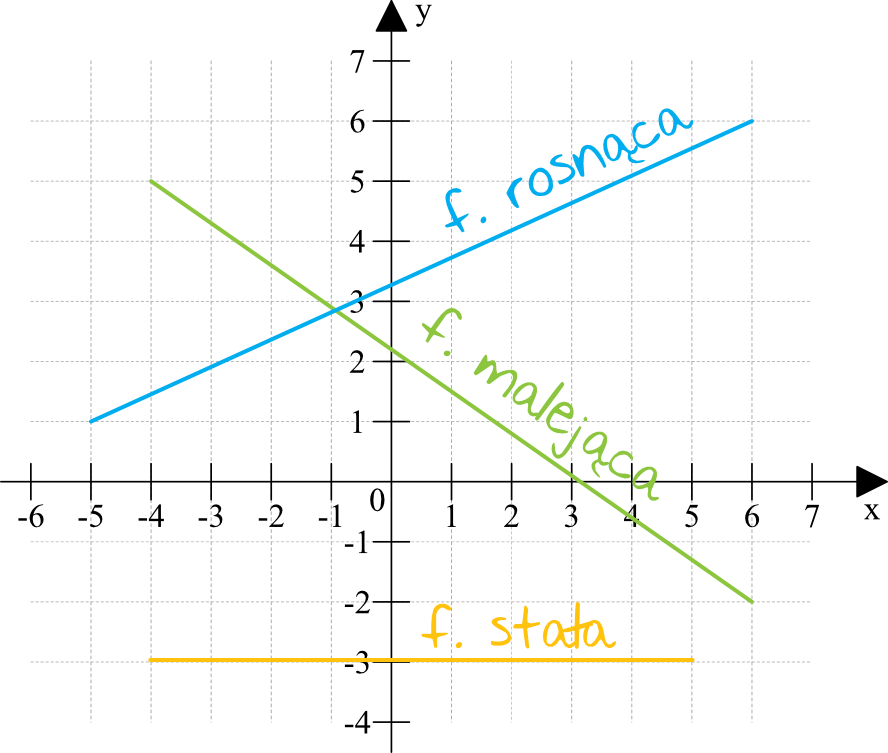
Na powyższym rysunku możemy dostrzec, że funkcja liniowa może być rosnąca, malejąca albo stała. Wszystko zależeć będzie właśnie od współczynnika kierunkowego \(a\), który znajduje się we wzorze w postaci \(f(x)=ax+b\):
Gdy \(a\gt0\) to funkcja liniowa jest rosnąca np. \(f(x)=3x+5\).
Gdy \(a\lt0\) to funkcja liniowa jest malejąca np. \(f(x)=-3x+5\).
Gdy \(a=0\) to funkcja liniowa jest stała np. \(f(x)=3\).
Kluczowymi punktami funkcji liniowej są miejsca przecięcia się z osią iksów (miejsca zerowe) oraz z osią igreków. Miejsce zerowe obliczymy przyrównując wzór funkcji do zera, natomiast miejsce przecięcia się z osią igreków odczytujemy ze współczynnika \(b\). Więcej informacji na ten temat znajdziesz w poniższych działach:

świetnie tłumaczysz, dziękuję!