Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości \(4\), jest równe:
\(256π\)
\(128π\)
\(48π\)
\(24π\)
Rozwiązanie:
Krok 1. Obliczenie długości promienia walca oraz jego wysokości.
Skoro w przekroju osiowym walca jest kwadrat o boku \(4\), to promień podstawy będzie równy połowie tej długości, czyli \(r=2\).
Wysokość walca będzie równa długości boku tego kwadratu, czyli \(H=4\).
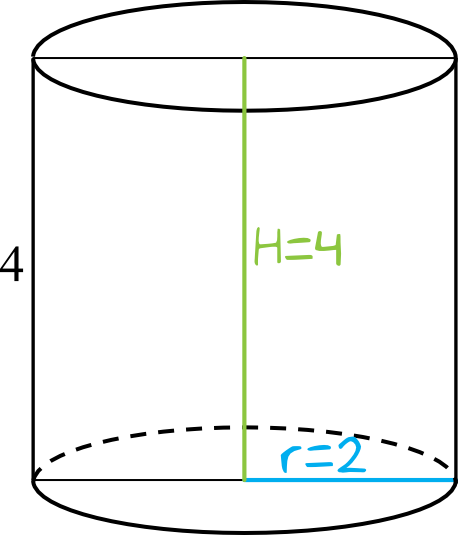
Krok 2. Obliczenie pola powierzchni całkowitej walca.
Pole powierzchni całkowitej walca obliczymy ze wzoru:
$$P_{c}=2πr^2+2πrH \\
P_{c}=2π\cdot2^2+2π\cdot2\cdot4 \\
P_{c}=2π\cdot4+2π\cdot8 \\
P_{c}=8π+16π \\
P_{c}=24π$$
Odpowiedź:
D. \(24π\)

