W trójkącie \(ABC\) poprowadzono dwusieczne kątów \(A\) i \(B\). Dwusieczne te przecinają się w punkcie \(P\). Uzasadnij, że kąt \(APB\) jest rozwarty.
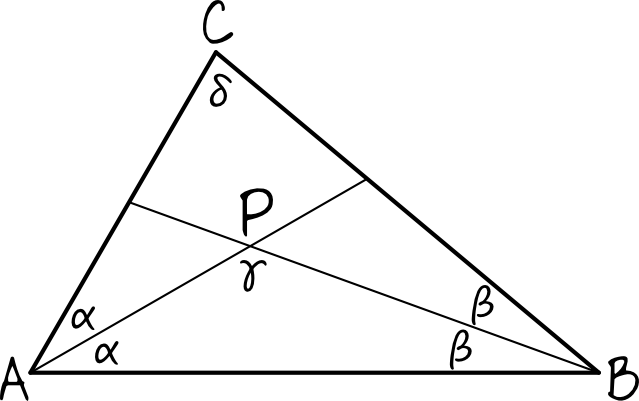
W tym zadaniu bardzo ważne jest to jak sobie oznaczymy poszczególne informacje. Oznaczmy więc sobie wszystko krok po kroku. Najpierw na rysunku nanieśmy kąty w naszym małym trójkącie \(APB\):
$$|\sphericalangle PAB|=α \\
|\sphericalangle PBA|=β \\
|\sphericalangle APB|=γ$$
Skoro dorysowane linie są dwusiecznymi, to także:
$$|\sphericalangle PAB|=α \\
|\sphericalangle PBC|=β$$
No i na koniec oznaczmy jeszcze ostatni kąt:
$$|\sphericalangle ACB|=δ$$
Suma kątów trójkąta \(ABC\) jest równa \(180°\). Czyli:
$$2α+2β+δ=180°$$
Kąt \(δ\) jest na pewno dodatni (nie wiemy ile ma stopni, ale jest na pewno dodatni). To oznacza, że suma kątów \(2α+2β\) jest mniejsza od \(180°\). Matematycznie możemy to zapisać jako:
$$2α+2β\lt180° \quad\bigg/:2 \\
α+β\lt90°$$
Nie wiemy jaka jest dokładna miara poszczególnych kątów, ale już wiemy, że suma kątów \(α+β<90°\). Spójrzmy teraz na mały trójkąt \(APB\). Tutaj suma kątów \(α+β+γ=180°\). Skoro suma \(α+β\) jest mniejsza od \(90°\), to kąt \(γ\) musi mieć więcej niż \(90°\) i w ten sposób możemy zakończyć nasz dowód.
Zadanie zostało udowodnione wykorzystując własności kątów w trójkątach.

