Dany jest kwadrat ABCD. Zbudowano trójkąty równoboczne ACE i BDF tak, że wierzchołek D kwadratu

Dany jest kwadrat $ABCD$. Zbudowano trójkąty równoboczne $ACE$ i $BDF$ tak, że wierzchołek $D$ kwadratu leży wewnątrz trójkąta $ACE$, a wierzchołek $C$ - wewnątrz trójkąta $BDF$. Odcinki $CE$ i $DF$ przecinają się w punkcie $G$ (jak na rysunku).

Wykaż, że $|CG|=|CF|$.

Rozwiązanie

Krok 1. Sporządzenie rysunku pomocniczego.
Skoro trójkąty $ACE$ i $BDF$ są równoboczne (czyli mają wszystkie kąty o mierze $60°$), a przekątne kwadratu tworzą z bokami kąty $45°$, to sytuacja z treści zadania wygląda następująco:
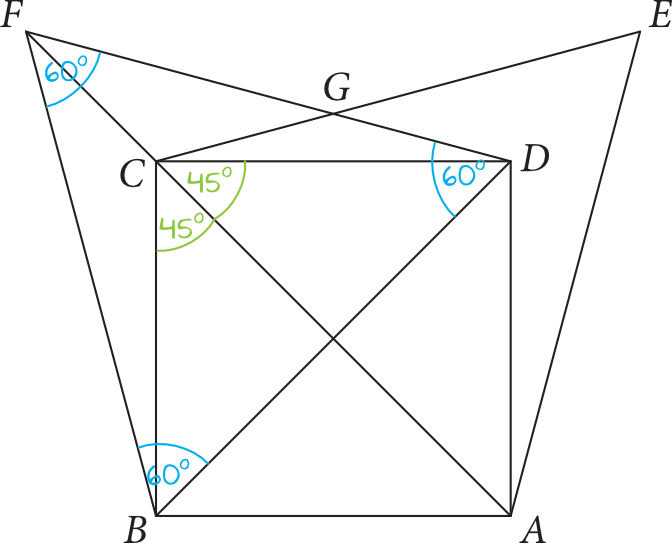
matura z matematyki

Krok 2. Obliczenie miar poszczególnych kątów.
Korzystając z rysunku możemy teraz obliczyć miarę np. kąta $CDF$:
$$|\sphericalangle CDF|=60°-45°=15°$$

Można więc powiedzieć, że w takim razie w trójkącie równoramiennym $CDG$ kąty przy podstawie mają $15°$, zatem kąt $CGD$ ma:
$$|\sphericalangle CGD|=180°-15°-15°=150°$$

Spójrzmy teraz na kąt $CGF$. Jest on kątem przystającym do kąta $CGD$, zatem jego miara jest równa:
$$|\sphericalangle CGF|=180°-150°=30°$$

Bardzo podobnie możemy obliczyć miarę kąta $FCG$.
$$|\sphericalangle FCG|=180°-45°-15°=120°$$

I teraz spoglądamy na trójkąt $CGF$. Znamy już dwie miary kątów w tym trójkącie i są to kąty o mierze $30°$ oraz $120°$, zatem trzeci kąt ma miarę:
$$|\sphericalangle FCG|=180°-120°-30°=30°$$

To oznacza, że kąty przy boku $FG$ mają jednakową miarę, czyli że trójkąt $CGF$ jest równoramienny. Skoro tak, to faktycznie $|CG|=|CF|$, co należało udowodnić.

Odpowiedź

Udowodniono, korzystając z własności kątów oraz trójkątów równoramiennych.