Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Kluczem do rozwiązania zadania jest dorysowanie odcinka \(CS\), który jest promieniem okręgu. Z własności stycznych do okręgu wiemy, że styczna tworzy z promieniem kąt prosty i to będzie dla nas bardzo ważna informacja w tym zadaniu dowodowym.
Drugą rzeczą, którą musimy dostrzec to fakt, że dorysowując odcinek \(CS\) utworzy nam się trójkąt równoramienny \(ASC\), którego ramiona są promieniami okręgu, a podstawą jest bok \(AC\). Co więcej, w treści zadania mamy tę długość podstawy opisaną jako \(|AC|=r\sqrt{3}\).
Nanosząc te wszystkie informacje oraz dorysowując jeszcze wysokość trójkąta równoramiennego \(ASC\) otrzymamy następującą sytuację:
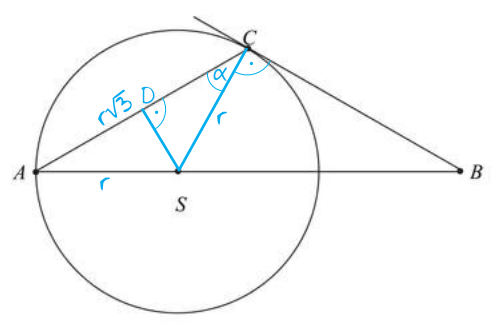
Krok 2. Obliczenie długości odcinka \(DC\).
Spójrzmy na trójkąt prostokątny \(DSC\). Długość odcinka \(DC\) jest równa połowie długości odcinka \(AC\) (bo wysokość padająca na podstawę dzieli podstawę na dwa równe odcinki). Możemy więc zapisać, że:
$$|DC|=\frac{1}{2}\cdot|AC| \\
|DC|=\frac{1}{2}\cdot r\sqrt{3} \\
|DC|=\frac{r\sqrt{3}}{2}$$
Krok 3. Obliczenie miary kąta \(ACS\).
Ponownie spoglądamy na trójkąt prostokątny \(DSC\). Wiemy, że \(|SC|=r\) oraz że \(|DC|=\frac{r\sqrt{3}}{2}\). Korzystając z funkcji trygonometrycznych (a konkretniej z cosinusa) możemy zapisać, że:
$$cosα=\frac{|DC|}{|SC|} \\
cosα=\frac{\frac{r\sqrt{3}}{2}}{r} \\
cosα=\frac{r\sqrt{3}}{2}:r \\
cosα=\frac{r\sqrt{3}}{2}\cdot\frac{1}{r} \\
cosα=\frac{\sqrt{3}}{2}$$
Z tablic trygonometrycznych możemy odczytać, że cosinus przyjmuje taką wartość dla kąta o mierze \(30°\), czyli \(|\sphericalangle ACS|=30°\).
Krok 4. Obliczenie miary kąta \(ACB\) i zakończenie dowodzenia.
Kąt \(ACB\) jest sumą kątów \(ACS\) oraz \(SCB\). Przed chwilą wyliczyliśmy, że \(|\sphericalangle ACS|=30°\), a z własności stycznych do okręgu wiemy, że \(|\sphericalangle SCB|=90°\). W związku z tym:
$$|\sphericalangle ACB|=30°+90°=120°$$
W ten sposób dowodzenie możemy uznać za zakończone.