Bryły obrotowe to bryły powstałe w wyniku obrotu figury płaskiej dookoła pewnej prostej, którą nazywamy osią obrotu. Najbardziej charakterystycznymi bryłami obrotowymi są stożek, walec oraz kula.
Przykłady brył obrotowych
W zależności od tego jaka figura płaska jest obracana mogą powstać różne bryły:
– walec otrzymamy w wyniku obrotu prostokąta
– stożek otrzymamy w wyniku obrotu trójkąta
– kulę otrzymamy w wyniku obrotu koła

Oś obrotu
Bryły obrotowe otrzymujemy poprzez obracanie figur płaskich. Prostą wokół której wykonujemy obrót nazywamy właśnie osią obrotu. Co ciekawe – daną figurę można obracać na wiele sposobów (np. wzdłuż jednego boku, wzdłuż drugiego boku, wzdłuż wysokości itd.). Ważne jest więc nie tylko co obracamy, ale i wokół czego ten obrót wykonujemy. Spójrzmy na poniższy przykład:
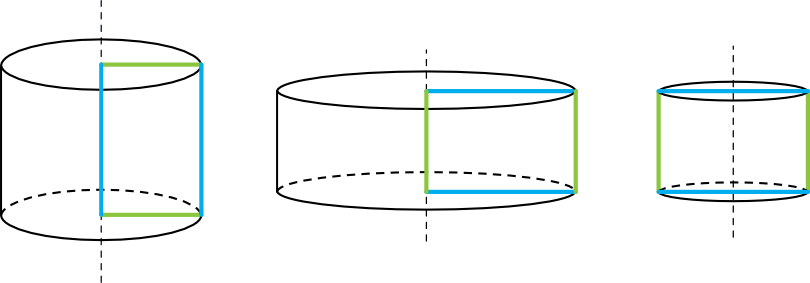
Na każdym powyższym rysunku obracaliśmy tą samą figurę (ten sam prostokąt), ale otrzymaliśmy tak naprawdę różne walce. Wszystko było więc zależne od tego wokół czego ten obrót wykonywaliśmy.
• Na pierwszym rysunku mamy walec powstały w wyniku obrotu wzdłuż dłuższego boku prostokąta.
• Na drugim rysunku mamy walec powstały w wyniku obrotu wzdłuż krótszego boku prostokąta.
• Na trzecim rysunku mamy walec powstały w wyniku obrotu wzdłuż jednej z osi symetrii prostokąta.
W przypadku trójkątów jest jeszcze ciekawiej, spójrzmy też na taki oto przykład:
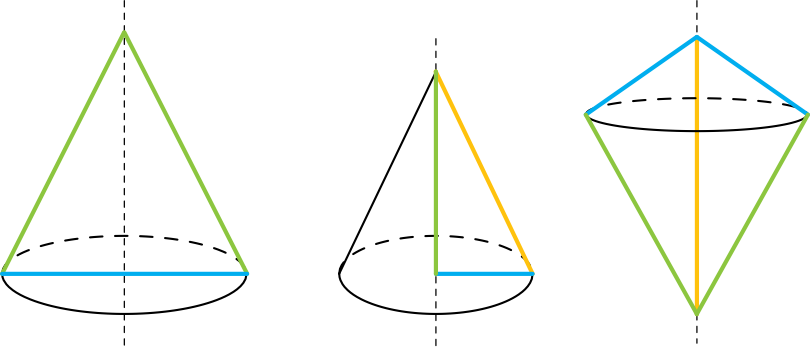
• Na pierwszym rysunku mamy sytuację w której trójkąt równoramienny jest obracany wokół swojej osi symetrii.
• Na drugim rysunku mamy trójkąt prostokątny, który jest obracany wokół jednej przyprostokątnej.
• Na trzecim rysunku mamy bardzo nietypową sytuację, bowiem tutaj trójkąt prostokątny obracany jest wokół swojej przeciwprostokątnej. W tym przypadku otrzymana bryła nie jest stożkiem. Jest to więc dla nas bardzo ciekawa obserwacja, bo okazuje się, że nie zawsze obracając trójkąt uda nam się uzyskać stożek.
Przekrój bryły obrotowej
Mówiąc o przekrojach bryły zazwyczaj spotkamy się z przekrojem osiowym lub poprzecznym, aczkolwiek przekroje mogą być też nieco bardziej nieregularne. Spójrzmy na kilka poniższych przykładów:
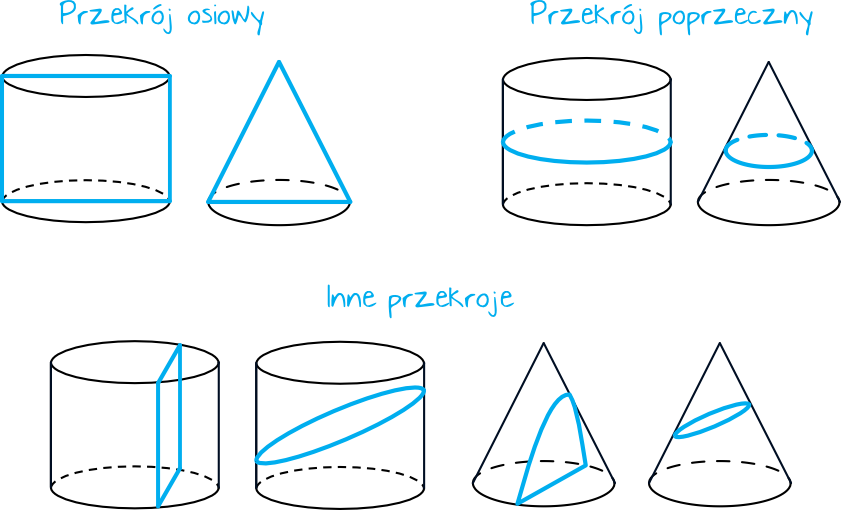
Nas na matematyce zazwyczaj będą interesować przekroje osiowe stożka i walca prawidłowego, zwłaszcza że to właśnie z nimi związane są najciekawsze własności:
• w przekroju osiowym walca znajdziemy prostokąt. Dolny bok tego prostokąta będzie średnicą podstawy, a boczny bok będzie wysokością całej bryły.
• w przekroju osiowym stożka znajdziemy trójkąt. Co ważne, będzie to zawsze trójkąt równoramienny. Podstawa tego trójkąta to będzie średnica podstawy, a ramionami trójkąta będą tak zwane tworzące stożka.
Omówienie najważniejszych brył obrotowych znajdziesz w poniższych tematach:
