Proste l i k przecinają się w punkcie A=(0,4). Prosta l wyznacza wraz z dodatnimi półosiami

Proste $l$ i $k$ przecinają się w punkcie $A=(0,4)$. Prosta $l$ wyznacza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu $8$, zaś prosta $k$ – trójkąt o polu $10$. Oblicz pole trójkąta, którego wierzchołkami są: punkt $A$ oraz punkty przecięcia prostych $l$ i $k$ z osią $Ox$.

Rozwiązanie:

Krok 1. Sporządzenie rysunku poglądowego.

Spróbujmy naszkicować sobie powyższą sytuację, co jak się za chwilę okaże będzie kluczem do rozwiązania tego zadania.

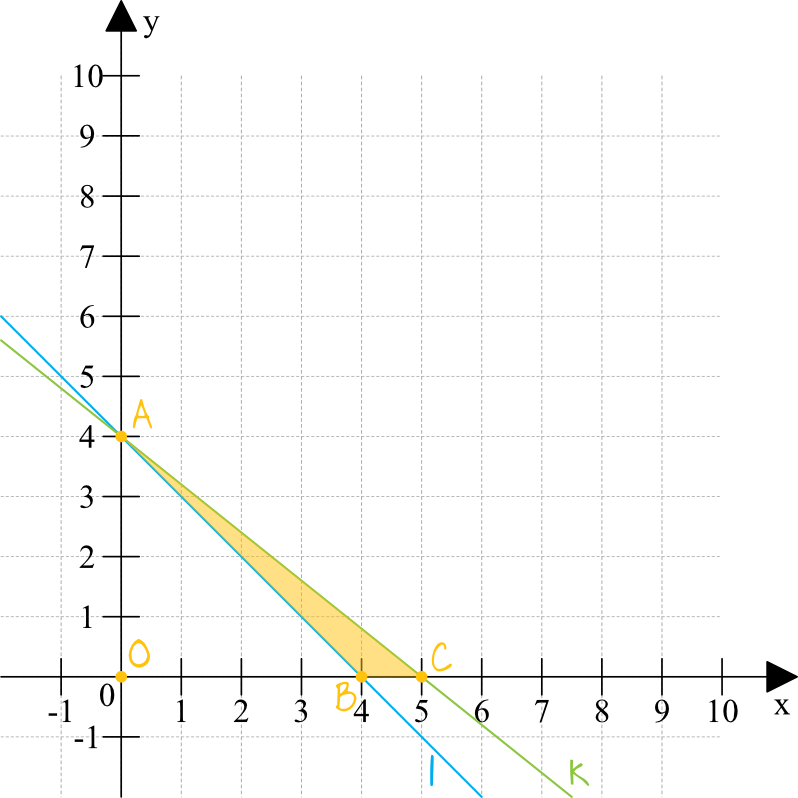
Dodatkowo oznaczyłem sobie początek układu współrzędnych jako punkt $O$, tak aby móc dokładnie nazywać poszczególne trójkąty które będziemy sobie za chwilę rozpatrywać.

Krok 2. Obliczenie pola trójkąta $ABC$.

Naszym zadaniem zgodnie z treścią zadania jest tak naprawdę obliczenie pola trójkąta $ABC$. Jego pole powierzchni jest różnicą między polami trójkątów $OCA$ oraz $OBA$, zatem:
$$P_{ABC}=P_{OCA}-P_{OBA}$$

Z treści zadania wynika, że $P_{OCA}=10$ oraz $P_{OBA}=8$, zatem:
$$P_{ABC}=10-8 \\
P_{ABC}=2$$

Odpowiedź:

$P_{ABC}=2$