Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy sobie szkic tej sytuacji, zaznaczając przy okazji miejsce przecięcia się przekątnych \(AC\) oraz \(BD\):
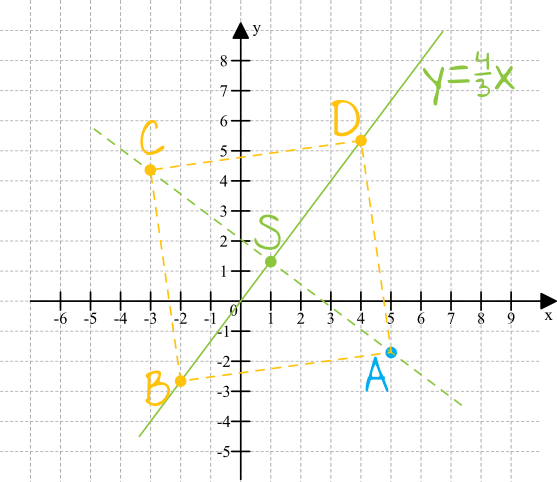
Na szkicu nie musimy zaznaczać tego pomarańczowego kwadratu - służy on jedynie lepszemu wyobrażeniu tego co za chwilę będziemy liczyć.
Krok 2. Wyznaczenie współczynnika kierunkowego \(a\) przekątnej \(AC\).
Przekątne kwadratu przecinają się zawsze pod kątem prostym. To oznacza, że przekątne \(AC\) oraz \(BD\) są względem siebie prostopadłe. Aby dwie były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Z treści zadania wiemy, że współczynnik kierunkowy \(a\) prostej \(BD\) jest równy \(\frac{4}{3}\), zatem współczynnik \(a\) prostej \(AC\) będzie równy \(-\frac{3}{4}\), bo \(-\frac{3}{4}\cdot\frac{4}{3}=-1\).
To z kolei oznacza, że równanie prostej \(AC\) możemy już zapisać jako \(y=-\frac{3}{4}x+b\). Do pełnego równania brakuje nam jeszcze współczynnika \(b\).
Krok 3. Wyznaczenie współczynnika \(b\) przekątnej \(AC\).
Wiemy już, że prosta AC wyraża się równaniem \(y=-\frac{3}{4}x+b\). Brakujący współczynnik \(b\) wyznaczymy podstawiając do tego równania współrzędne jednego z punktów, który należy do tej prostej. Takim punktem jest punkt \(A=\left(5,-\frac{5}{3}\right)\), zatem:
$$y=-\frac{3}{4}x+b \\
-\frac{5}{3}=-\frac{3}{4}\cdot5+b \\
-\frac{5}{3}=-\frac{15}{4}+b \\
-\frac{20}{12}=-\frac{45}{12}+b \\
b=\frac{25}{12}$$
To oznacza, że nasza prosta \(AC\) wyraża się równaniem \(y=-\frac{3}{4}x+\frac{25}{12}\).
Krok 4. Wyznaczenie współrzędnych miejsca przecięcia się przekątnych.
Z geometrycznej interpretacji układu równań wiemy, że kiedy zbudujemy układ równań składający się z dwóch prostych, to rozwiązaniem tego układu będą współrzędne punktu ich przecięcia. Skoro tak, to wyznaczmy miejsce przecięcia się naszych przekątnych:
\begin{cases}
y=\frac{4}{3}x \\
y=-\frac{3}{4}x+\frac{25}{12}
\end{cases}
Korzystając z metody podstawiania otrzymamy:
$$\frac{4}{3}x=-\frac{3}{4}x+\frac{25}{12} \quad\bigg/\cdot12 \\
16x=-9x+25 \\
25x=25 \\
x=1$$
Znając wartość iksa, możemy bez problemu poznać igreka. W tym celu wystarczy do dowolnego równania z układu równań (np. pierwszego) podstawić wyznaczone x=1, zatem:
$$y=\frac{4}{3}x \\
y=\frac{4}{3}\cdot1 \\
y=\frac{4}{3}$$
To oznacza, że nasze przekątne przecinają się w punkcie \(S=\left(1;\frac{4}{3}\right)\).
Krok 5. Obliczenie długości odcinka \(AS\) i przekątnej \(AC\).
Odcinek \(AS\) jest połową długości przekątnej naszego kwadratu. Znamy współrzędne punktu \(A\) oraz \(S\), zatem korzystając ze wzoru na długość odcinka możemy zapisać, że:
$$|AS|=\sqrt{(x_{S}-x_{A})^2+(y_{S}-y_{A})^2} \\
|AS|=\sqrt{(1-5)^2+\left(\frac{4}{3}-\left(-\frac{5}{3}\right)\right)^2} \\
|AS|=\sqrt{(-4)^2+(-3)^2} \\
|AS|=\sqrt{16+9} \\
|AS|=\sqrt{25} \\
|AS|=5$$
Przekątne kwadratu przecinają się w połowie swojej długości, zatem odcinek \(AC\) będzie dwukrotnie większy od odcinka \(AS\). Skoro tak, to:
$$|AC|=2\cdot5 \\
|AC|=10$$
Krok 6. Obliczenie pola powierzchni kwadratu \(ABCD\).
Znając długość przekątnej moglibyśmy oczywiście wyznaczyć długość boku kwadratu, a dopiero potem pole powierzchni, ale możemy też postąpić nieco sprytniej i skorzystać z innego wzoru na pole kwadratu (takiego samego jak pole rombu):
$$P=\frac{1}{2}\cdot e\cdot f \\
P=\frac{1}{2}\cdot10\cdot10 \\
P=50$$