Rozwiązanie
Krok 1. Ułożenie nierówności.
Aby sprawdzić ile jest wyrazów niedodatnich (czyli ujemnych lub równych zero) musimy sprawdzić kiedy \(3n^2-25n\) będzie mniejsze lub równe \(0\). W związku z tym musimy rozwiązać nierówność:
$$3n^2-25n\le0$$
Krok 2. Rozwiązanie nierówności.
Możemy tę nierówność rozwiązać korzystając z delty (pamiętając o tym, że tutaj współczynnik \(c=0\)), ale znacznie prościej będzie będzie po prostu wyłączyć \(n\) przed nawias:
$$n(3n-25)\le0$$
Teraz do rozwiązania nierówności musimy wyznaczyć miejsca zerowe, czyli sprawdzić kiedy \(n(3n-25)\) jest równe \(0\). Wystarczy więc przyrównać \(n\) oraz \(3n-25\) do zera:
$$n=0 \quad\lor\quad 3n-25=0 \\
n=0 \quad\lor\quad 3n=25 \\
n=0 \quad\lor\quad n=8\frac{1}{3}$$
Znając miejsca zerowe, możemy przystąpić do rysowania paraboli (ramiona paraboli będą skierowane do góry):
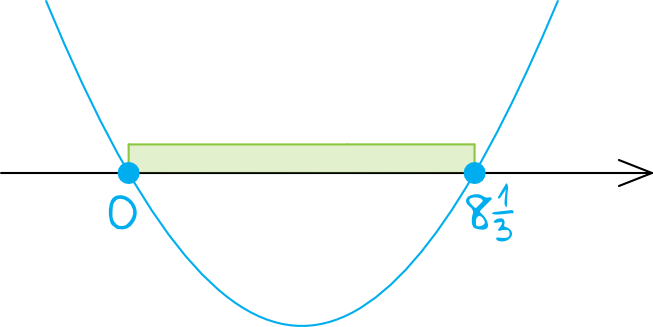
Interesują nas wartości mniejsze lub równe zero, czyli patrzymy się na to, co znajduje się pod osią lub na osi. To oznacza, że \(n\in\langle0;8\frac{1}{3}\rangle\).
Krok 3. Ustalenie liczby niedodatnich wyrazów.
Wiemy, że w ciągach \(n\) jest liczbą naturalną \(n\ge1\). Zastanówmy się więc, jakie liczby mieszczą się w przedziale \(n\in\langle0;8\frac{1}{3}\rangle\). Będą to:
$$1,2,3,4,5,6,7,8$$
To oznacza, że nasz ciąg ma \(8\) wyrazów niedodatnich.