Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
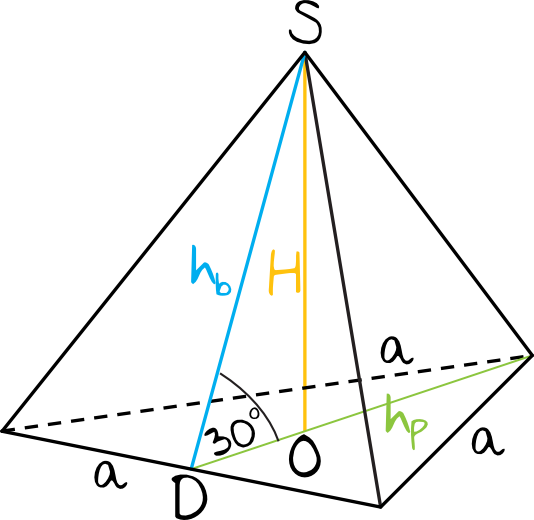
Krok 2. Obliczenie wysokości podstawy.
Z własności okręgów opisanych na trójkącie wynika, że długość promienia takiego okręgu jest równa \(\frac{2}{3}\) wysokości trójkąta. Z treści zadania wiemy, że \(R=2\sqrt{3}\), czyli:
$$R=\frac{2}{3}h_{p} \\
2\sqrt{3}=\frac{2}{3}h_{p} \quad\bigg/\cdot\frac{3}{2} \\
h_{p}=\frac{6\sqrt{3}}{2} \\
h_{p}=3\sqrt{3}$$
Krok 3. Obliczenie długości krawędzi podstawy.
W podstawie naszej bryły znajduje się trójkąt równoboczny (bo ostrosłup jest prawidłowy). Korzystając ze wzoru na wysokość trójkąta równobocznego wyliczymy długość jego boku:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
3\sqrt{3}=\frac{a\sqrt{3}}{2} \\
6\sqrt{3}=a\sqrt{3} \\
a=6$$
Krok 4. Obliczenie długości odcinka \(DO\).
Odcinek \(DO\) jest równy \(\frac{1}{3}\) długości wysokości trójkąta. Wynika to z własności ostrosłupów - wysokość ostrosłupa dzieli nam wysokość podstawy właśnie na dwa odcinki o długości \(\frac{1}{3}h_{p}\) oraz \(\frac{2}{3}h_{p}\). To oznacza, że:
$$|DO|=\frac{1}{3}\cdot3\sqrt{3} \\
|DO|=\sqrt{3}$$
Krok 5. Obliczenie wysokości ostrosłupa oraz wysokości ściany bocznej.
Spójrzmy teraz na trójkąt prostokątny \(DOS\). To właśnie z niego obliczymy wysokość całej bryły. Możemy to zrobić albo z własności trójkątów o kątach \(30°, 60°, 90°\), albo po prostu korzystając z tangensa:
$$tg30°=\frac{H}{|DO|} \\
\frac{\sqrt{3}}{3}=\frac{H}{\sqrt{3}} \quad\bigg/\cdot\sqrt{3} \\
H=\frac{3}{3} \\
H=1$$
Krok 6. Obliczenie wysokości ściany bocznej.
Musimy obliczyć jeszcze wysokość ściany bocznej, bo przyda nam się to do obliczenia pola powierzchni bocznej. Tutaj możemy skorzystać z własności trójkątów o kątach \(30°, 60°, 90°\), z funkcji trygonometrycznych, albo nawet z Twierdzenia Pitagorasa. Mamy więc pełną dowolność. Obliczmy to może z funkcji trygonometrycznych, a konkretniej z sinusa:
$$sin30°=\frac{H}{h_{b}} \\
\frac{1}{2}=\frac{1}{h_{b}} \\
\frac{1}{2}h_{b}=1 \\
h_{b}=2$$
Krok 7. Obliczenie objętości bryły.
Mamy już wszystkie potrzebne informacje, zatem możemy przystąpić do obliczenia objętości bryły. W podstawie możemy skorzystać ze wzoru na pole trójkąta równobocznego, zatem:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot\frac{a^2\sqrt{3}}{4}\cdot H \\
V=\frac{1}{3}\cdot\frac{6^2\sqrt{3}}{4}\cdot1 \\
V=\frac{1}{3}\cdot\frac{36\sqrt{3}}{4} \\
V=\frac{1}{3}\cdot9\sqrt{3} \\
V=3\sqrt{3}$$
Krok 8. Obliczenie pola powierzchni bocznej.
Na pole powierzchni bocznej składają się trzy trójkąty w których \(a=6\) oraz \(h_{b}=2\), zatem:
$$P_{b}=3\cdot\frac{1}{2}ah \\
P_{b}=3\cdot\frac{1}{2}\cdot6\cdot2 \\
P_{b}=3\cdot3\cdot2 \\
P_{b}=18$$