Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Równanie prostej. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) 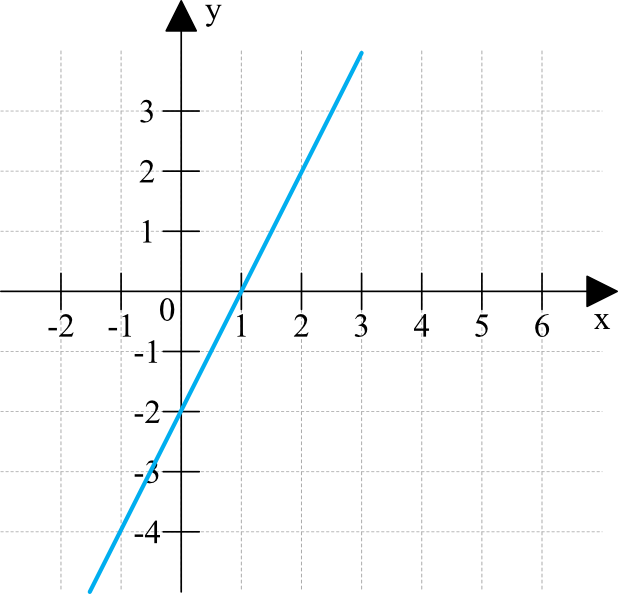
Równanie powyższej prostej to:
Zadanie 2. (1pkt) Współczynnik kierunkowy prostej określonej równaniem \(2x+3y-6=0\) wynosi:
Zadanie 3. (1pkt) Co możemy powiedzieć o prostej określonej równaniem \(y=-3x+\frac{1}{4}\)?
Zadanie 4. (1pkt) Aby punkt \(P=(-3;2)\) należał do prostej o równaniu \(y=ax-4\), to współczynnik \(a\) musi być równy:
Zadanie 5. (1pkt) Proste \(y=-2x+2\) oraz \(y=4x-1\) przecinają się w punkcie o współrzędnych:
Zadanie 6. (1pkt) Równaniem prostej przechodzącej przez punkty \(A=(2;-5)\) oraz \(B=(-3;15)\) jest \(y=-4x+3\).
Zadanie 7. (1pkt) Prosta określona równaniem \(2x-y-7=0\) i prosta \(y=2x-7\), to te same proste, tylko że za pierwszym razem mamy równanie w postaci ogólnej, a za drugim w postaci kierunkowej.
Zadanie 8. (1pkt) Dane są trzy punkty: \(A=(-2;-9)\), \(B=(3;1)\) oraz \(C=(6;7)\). Jaś twierdzi, że te trzy punkty leżą na jednej prostej. Małgosia uważa, że jeden z tych punktów lekko odstaje i przez to te trzy punkty nie znajdują się na jednej prostej. Kto ma rację?
Zadanie 9. (1pkt) Jeżeli punkty \(A=(2;y_{A})\) oraz \(B=(x_{B};-8)\) należą do prostej \(y=3x+1\), to suma \(y_{A}+x_{B}\) będzie równa:
Zadanie 10. (1pkt) Współczynnik kierunkowy \(a\) prostej \(y=ax+b\) przechodzącej przez punkty \(A=\left(3\frac{1}{3};2\frac{1}{4}\right)\) oraz \(B=\left(\frac{1}{3};2\right)\) jest równy:
