Rozwiązanie
Krok 1. Ułożenie nierówności.
Aby dowiedzieć się ile jest dodatnich wyrazów tego ciągu to musimy rozwiązać nierówność:
$$-n^2+16\gt0 \quad\bigg/\cdot(-1) \\
n^2-16\lt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Teraz musimy obliczyć miejsca zerowe wielomianu, przyrównując wartość \(n^2-16\) do zera. Możemy to zrobić standardową deltą, ale to jest jedna z tych nierówności którą da się obliczyć niemalże w pamięci:
$$n^2-16=0 \\
n^2=16 \\
n=4 \quad\lor\quad n=-4$$
Krok 3. Szkicowanie wykresu paraboli.
Znając miejsca zerowe wielomianu możemy przystąpić do szkicowania wykresu paraboli. Ramiona paraboli będą skierowane do góry, bo przed \(n^2\) nie ma żadnej ujemnej wartości:
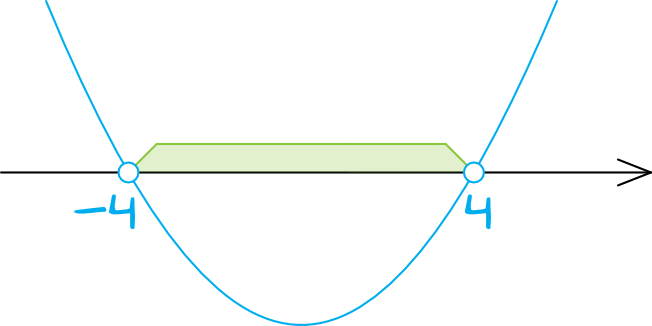
Krok 4. Odczytanie i interpretacja rozwiązania.
Szukamy argumentów, dla których nierówność przyjmuje wartości mniejsze od zera. W związku z tym: \(n\in(-4;4)\).
Jak teraz zinterpretować to rozwiązanie? Z treści zadania (i ogólnie z wiedzy o ciągach) wiemy, że \(n\ge1\). Wiemy też, że \(n\) jest liczbą naturalną. W związku z tym skoro nasze \(n\) musi być większe lub równe \(1\) i jednocześnie musi się mieścić w przedziale \(n\in(-4;4)\), to mamy tylko trzy liczby które spełniają te warunki: \(n=1, n=2, n=3\). W związku z tym ten ciąg ma tylko trzy dodatnie wyrazy.