Rozwiązanie
To zadanie rozwiążemy sobie na dwa sposoby, ponieważ istnieje tutaj bardzo szybka droga do poznania prawidłowej odpowiedzi.
I sposób - obliczając liczbę zdarzeń elementarnych i sprzyjających.
Krok 1. Obliczenie liczby wszystkich zdarzeń elementarnych.
Z pierwszego zbioru możemy wylosować jedną z sześciu liczb. Z drugiego zbioru możemy wylosować jedną z czterech liczb. W związku zgodnie z regułą mnożenia wszystkich zdarzeń elementarnych będziemy mieć:
$$|Ω|=6\cdot4=24$$
Krok 2. Obliczenie liczby zdarzeń sprzyjających.
Musimy teraz ustalić jaka para liczb będzie tworzyć zdarzenie sprzyjające, zatem musimy ustalić które liczby ze zbioru \(A\) oraz \(B\) pasują nam do warunków zadania. Aby funkcja była rosnąca, to współczynnik kierunkowy \(a\) musi być dodatni. To oznacza, że z pierwszego zbioru interesują nas tylko liczby \(1,2,3\).
Teraz musimy ustalić jakie liczby interesują nas ze zbioru \(B\), a wpływ na to mieć będzie informacja mówiąca o tym, iż funkcja ma mieć dodatnie miejsca zerowe. Co to oznacza, że miejsca zerowe są dodatnie? Jeżeli funkcja przecina oś iksów dla np. \(x=-2\), to znaczy że miejsce zerowe jest ujemne (taki przypadek nas nie interesuje). Jeżeli funkcja przecina oś iksów dla np. \(x=3\) to wtedy miejsce zerowe jest dodatnie. Jak więc ustalić kiedy funkcja osiąga dodatnie miejsce zerowe?
Aby funkcja liniowa (która jest rosnąca) miała dodatnie miejsce zerowe dodatnie, to musi przecinać oś igreków w ujemnej wartości (czyli pod osią iksów), nie ma innej możliwości. O miejscu przecięcia się z osią igreków informuje nas współczynnik \(b\) i już po tej prostej analizie wiemy, że musi on być ujemny. To by oznaczało, że ze zbioru \(B\) interesowałaby nas jedynie wartość \(-1\).
Jeżeli jednak nie dostrzegliśmy tej własności, to możemy podejść do zagadnienia z innej strony. Aby wyznaczyć miejsce zerowe funkcji (jakiekolwiek) to musimy przyrównać wzór funkcji do zera. Zatem:
$$ax+b=0 \\
ax=-b \\
x=\frac{-b}{a}$$
My musimy mieć to miejsce zerowe większe od zera, czyli interesuje nas sytuacja w której:
$$\frac{-b}{a}\gt0$$
Skoro w naszym przypadku \(a\) jest dodatnie, to aby wyrażenie \(\frac{-b}{a}\) było większe od zera, to w liczniku musimy mieć także liczbę dodatnią. To oznacza, że \(b\) musi być liczbą ujemną. Z podanych liczb w zbiorze \(B\) tylko liczba \(-1\) spełnia ten warunek.
Skoro więc ze zbioru \(A\) interesują nas liczby \(1,2,3\), a ze zbioru \(B\) interesuje nas jedynie \(-1\), to zdarzeniami sprzyjającymi będą:
$$(1;-1), (2;-1), (3;-1)$$
Są to więc tylko trzy pary liczb, zatem \(|A|=3\).
Krok 3. Obliczenie prawdopodobieństwa.
$$P(A)=\frac{|A|}{|Ω|}=\frac{3}{24}=\frac{1}{8}$$
II sposób - dostrzegając własności wykresu funkcji liniowej.
Moglibyśmy dostrzec, że aby funkcja była rosnąca i miała dodatnie miejsce zerowe, musi ona wyglądać mniej więcej w ten sposób:
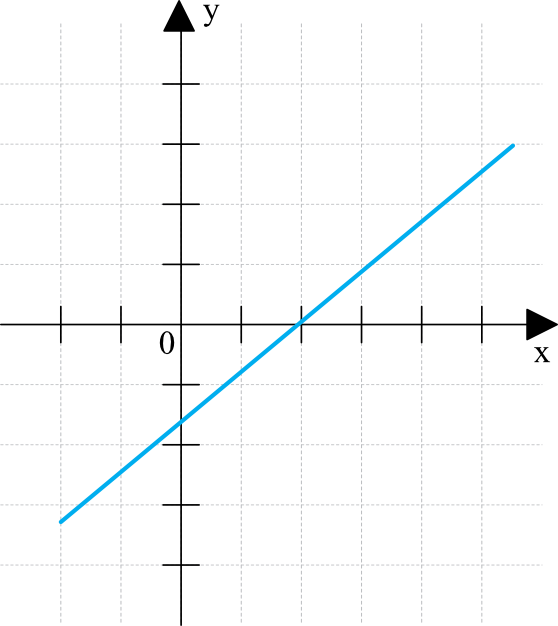
Funkcja ma być rosnąca, czyli współczynnik \(a\) musi być dodatni. Z sześciu podanych liczb tylko trzy są dodatnie, więc prawdopodobieństwo wylosowania dodatniego współczynnika \(a\) jest równe \(\frac{1}{2}\). Z analizy wykresu wynika też, że współczynnik \(b\) musi być ujemny, bo prosta przetnie nam oś \(OY\) dla ujemnej wartości \(y\). Tylko jedna z czterech proponowanych liczb jest ujemna, więc szanse wylosowania ujemnej liczby wyniosą \(\frac{1}{4}\). Prawdopodobieństwo wylosowania więc jednocześnie odpowiedniej liczby \(a\) oraz \(b\) będzie równe iloczynowi wyznaczonych przed chwilą prawdopodobieństw:
$$p=\frac{1}{2}\cdot\frac{1}{4}=\frac{1}{8}$$