Zbiorem wartości funkcji kwadratowej f(x)=x^2-4 jest

Zbiorem wartości funkcji kwadratowej \(f(x)=x^2-4\) jest:

\(\langle-4;+\infty)\)

\(\langle-2;+\infty)\)

\(\langle2;+\infty)\)

\(\langle4;+\infty)\)

Rozwiązanie:

To zadanie najprościej jest rozwiązać metodą graficzną. Narysujmy sobie wykres funkcji \(g(x)=x^2\) (funkcja niebieska), a następnie przekształcamy ją przesuwając parabolę o cztery jednostki do dołu, tak aby nowa parabola reprezentowała funkcję \(f(x)=x^2-4\) (funkcja zielona).

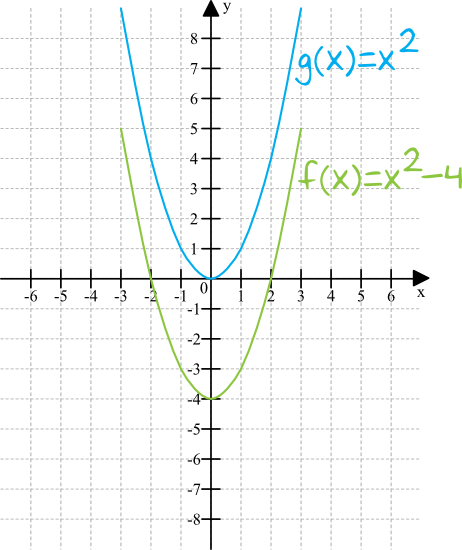
Teraz z wykresu bardzo łatwo możemy odczytać, że zbiorem wartości tej funkcji kwadratowej jest \(\langle-4;+\infty)\).

Odpowiedź:

A. \(\langle-4;+\infty)\)