Matura 2023 i 2024 wprowadza bardzo dużo zmian, zarówno w samej formule egzaminu jak i w podstawie programowej. W tym temacie omówię zmiany, które zaszły na matematyce, pokazując Wam czego możemy się spodziewać po nowej formule egzaminu na poziomie podstawowym.
Na początek bardzo ważna informacja, ponieważ bardzo wiele osób nie zdaje sobie z tego sprawy – uczniowie liceum oraz technikum będą pisać w 2023 zupełnie różne matury:
– uczniowie liceum będą pisać maturę 2023 i 2024 na nowych zasadach, które zaraz sobie omówimy;
– uczniowie technikum będą pisać maturę 2023 na starych zasadach, natomiast nowe zasady obejmą tutaj dopiero maturę 2024.
Od wielu lat (pomijając np. okresy pandemii) arkusz wyglądał zazwyczaj tak, że mieliśmy 25 zadań zamkniętych ABCD i 9 zadań otwartych. Według zasad nowej matury, możemy spodziewać się 20-25 zadań zamkniętych i 9-15 zadań otwartych. Teoretycznie w dalszym ciągu możliwy jest znany ze starej matury podział na 25 zadań zamkniętych i 9 zadań otwartych, choć patrząc na widełki, należy się spodziewać raczej mniejszej niż dotychczas liczby zadań zamkniętych i większej zadań otwartych. Wiele wskazuje też na to, że nie będziemy już mieć najpierw zadań zamkniętych, a potem otwartych – teraz zadania prawdopodobnie będą się przeplatać.
Zmienia się też czas przeznaczony na rozwiązywanie arkusza. Teraz potrwa on 180 minut (do tej pory było to 170 minut).
Niezmienna pozostaje liczba punktów do zdobycia – w dalszym ciągu będzie to 50 punktów (połowa z zadań zamkniętych, połowa z zadań otwartych). Aby zdać maturę trzeba zdobyć minimum 30%, czyli 15 punktów.
Najważniejsze zmiany w maturze możemy podzielić na dwie kategorie:
– nowe typy zadań
– wymagania egzaminacyjne
Zdecydowanie najwięcej zamieszania wzbudza ten ostatni punkt, czyli nowa podstawa egzaminacyjna, która została już kolejny raz zmieniona. Efekt tych zmian jest taki, że w 2023 i 2024 uczniowie będą pisać maturę na nowych zasadach, ale z nieco okrojonym programem. Pełna podstawa programowa zacznie obowiązywać od 2025 roku, no chyba, że znowu coś się zmieni.
Do tej pory na maturze mieliśmy zadania zamknięte z odpowiedziami ABCD oraz zadania otwarte. Teraz katalog możliwych zadań znacząco się powiększa.
Wśród zadań zamkniętych znajdą się m.in.:
Przykładowe zadanie:
Wartość wyrażenia \(2021:\left(1-\frac{1}{2022}\right)-\left(1-\frac{2022}{2021}\right):\frac{1}{2021}\) jest równa:
- Rozwiązanie:
Pamiętaj, że liczbę \(1\) możemy zapisać jako ułamek, w którym licznik i mianownik są jednakowe. W tym zadaniu przyda nam się zamiana \(1=\frac{2021}{2021}\) oraz \(1=\frac{2021}{2021}\). Teraz korzystając z działań na ułamkach, możemy zapisać, że:
$$2021:\left(1-\frac{1}{2022}\right)-\left(1-\frac{2022}{2021}\right):\frac{1}{2021}= \\
=2021:\left(\frac{2022}{2022}-\frac{1}{2022}\right)-\left(\frac{2021}{2021}-\frac{2022}{2021}\right):\frac{1}{2021} =\\
=2021:\frac{2021}{2022}-\left(-\frac{1}{2021}\right):\frac{1}{2021}= \\
=2021:\frac{2021}{2022}+\frac{1}{2021}:\frac{1}{2021}= \\
=2021\cdot\frac{2022}{2021}+\frac{1}{2021}\cdot\frac{2021}{1}=2022+1=2023$$ - Odpowiedź:
D. \(2023\)
Przykładowe zadanie:
Dana jest liczba \(x=a-(\sqrt{3}-\sqrt{2})^2\), gdzie \(a\) należy do zbioru \(\mathbb{R}\) liczb rzeczywistych. W rozwiązaniu zadania uwzględnij fakt, że liczby \(\sqrt{3}\) oraz \(\sqrt{2}\cdot\sqrt{3}\) są niewymierne.
Dokończ zdanie. Zaznacz dwie odpowiedzi, tak aby dla każdej z nich dokończenie zdania było prawdziwe.
Liczba \(x\) jest wymierna dla:
- Rozwiązanie:
Krok 1. Obliczenie wartości liczby \(x\).
Spróbujmy obliczyć wartość liczby \(x\) wykonując występujące w niej potęgowanie. Korzystając ze wzorów skróconego mnożenia możemy zapisać, że:
$$x=a-(\sqrt{3}-\sqrt{2})^2 \\
x=a-(\sqrt{3})^2-2\cdot\sqrt{3}\cdot\sqrt{2}+(\sqrt{2})^2 \\
x=a-(3-2\sqrt{6}+2) \\
x=a-(5-2\sqrt{6}) \\
x=a-5+2\sqrt{6}$$Krok 2. Ustalenie, kiedy liczba \(x\) jest wymierna.
Musimy się teraz zastanowić, kiedy \(a-5+2\sqrt{6}\) da wynik wymierny. Aby tak się stało, to w wartości liczby \(a\) musi się pojawić \(-2\sqrt{6}\) (wtedy te pierwiastki się „zniosą”) i w zapisie tej liczby nie mogą nam oczywiście pojawić się inne nowe pierwiastki.Od razu możemy stwierdzić, że poprawna jest odpowiedź E, czyli \(a=-2\sqrt{6}+12,5\), bowiem to jest dokładnie to, czego szukamy. Musimy jeszcze wybrać drugą odpowiedź. Na pewno nie będzie to A, B, D oraz G (bo brakuje tu wartości \(-2\sqrt{6}\)). Do rozpatrzenia zostaje nam C oraz F. Rozpiszmy sobie każdy z tych wariantów:
Odp. C. \((\sqrt{2}-\sqrt{3})^2+0,3=2-2\sqrt{6}+3+0,3=5,3-2\sqrt{6}\)
Ta odpowiedź nam pasuje.Odp. F. \((\sqrt{2}-\sqrt{3})^2-2\sqrt{6}=2-2\sqrt{6}+3-2\sqrt{6}=5-4\sqrt{6}\)
Ta odpowiedź nam nie pasuje, bo jest tutaj \(-4\sqrt{6}\).Podsumowując, pasującymi odpowiedziami będą C oraz E.
- Odpowiedź:
C. \(a=(\sqrt{2}-\sqrt{3})^2+0,3\) oraz E. \(a=-2\sqrt{6}+12,5\)
Przykładowe zadanie:
Pensja pana \(X\) jest o \(50\%\) wyższa od średniej krajowej, a pensja pana \(Y\) jest o \(40\%\) niższa od średniej krajowej.
Dokończ zdania. Zaznacz odpowiedź spośród A-D oraz odpowiedź spośród E-H.
1. Pensja pana \(X\) jest wyższa od pensji pana \(Y\):
2. Pensja pana \(Y\) jest niższa od pensji pana \(X\):
- Rozwiązanie:
Krok 1. Wprowadzenie oznaczeń do treści zadania.
Wprowadźmy do naszego zadania następujące oznaczenia:
\(s\) – średnia pensja krajowa
\(1,5s\) – średnia pensja Pana \(X\)
\(0,6s\) – średnia pensja Pana \(Y\)Od razu możemy też zapisać, że Pan \(X\) zarabia o \(1,5s-0,6s=0,9s\) więcej niż Pan \(Y\).
Krok 2. Obliczenie procentowej różnicy wynagrodzenia.
Pensja pana \(X\) jest wyższa od pensji pana \(Y\) o:
$$\frac{0,9s}{0,6s}=1,5=150\%$$Pensja pana \(Y\) jest mniejsza od pensji pana \(X\) o:
$$\frac{0,9s}{1,5s}=0,6=60\%$$ - Odpowiedź:
C. o \(150\%\) pensji pana \(Y\) oraz E. o \(60\%\) pensji pana \(X\)
Przykładowe zadanie:
Dany jest kąt o mierze \(\alpha\) taki, że \(sin\alpha=\frac{4}{5}\) oraz \(90°\lt\alpha\lt180°\).
Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Dla kąta \(\alpha\) spełnione jest równanie \(cos\alpha=-\frac{3}{5}\) | P | F |
| Dla kąta \(\alpha\) spełnione jest równanie \(|tg\alpha|=\frac{3}{4}\) | P | F |
- Rozwiązanie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Korzystając z jedynki trygonometrycznej możemy zapisać, że:
$$sin^2\alpha+cos^2\alpha=1 \\
\left(\frac{4}{5}\right)^2+cos^2\alpha=1 \\
\frac{16}{25}+cos^2\alpha=1 \\
cos^2\alpha=\frac{9}{25} \\
cos\alpha=\frac{3}{5} \quad\lor\quad cos\alpha=-\frac{3}{5}$$Z treści zadania wynika, że kąt \(\alpha\) jest kątem rozwartym. Cosinus dla takich kątów przyjmuje wartości ujemne, stąd też rozwiązanie \(cos\alpha=\frac{3}{5}\) musimy odrzucić. Zostaje nam zatem, że \(cos\alpha=-\frac{3}{5}\), czyli zdanie jest prawdą.
Krok 2. Ocena prawdziwości drugiego zdania.
Z treści zadania wiemy, że \(sin\alpha=\frac{4}{5}\). Dodatkowo obliczyliśmy sobie przed chwilą, że \(cos\alpha=-\frac{3}{5}\). Korzystając zatem ze wzoru na tangens, możemy zapisać, że:
$$tg\alpha=\frac{sin\alpha}{cos\alpha} \\
tg\alpha=\frac{\frac{4}{5}}{-\frac{3}{5}} \\
tg\alpha=\frac{4}{5}\cdot\left(-\frac{5}{3}\right) \\
tg\alpha=-\frac{4}{3}$$To oznacza, że \(|tg\alpha|=\frac{4}{3}\), więc zdanie jest fałszem.
- Odpowiedź:
Prawda oraz Fałsz
Przykładowe zadanie:
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=3x^2+bx-5\) dla każdej liczby rzeczywistej \(x\). Współczynnik \(b\) jest liczbą rzeczywistą mniejszą od zera.
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Funkcja \(f\):
| A. ma dwa rzeczywiste miejsca zerowe, | ponieważ | 1. \(b^2+60\gt0\) |
| B. ma jedno rzeczywiste miejsce zerowe, | 2. \(b^2+60=0\) | |
| C. nie ma rzeczywistych miejsc zerowych, | 3. \(b^2+60\lt0\) |
- Rozwiązanie:
O tym, ile miejsc zerowych ma dana funkcja, decyduje tak zwana delta, którą obliczamy rozwiązując równania kwadratowe. Wypiszmy zatem współczynniki funkcji \(f(x)=3x^2+bx-5\) i obliczmy deltę:
Współczynniki: \(a=3,\;b=b,\;c=-5\)
$$Δ=b^2-4ac=b^2-4\cdot3\cdot(-5)=b^2-(-60)=b^2+60$$Z treści zadania wynika, że \(b\) jest liczbą mniejszą od zera. Taka liczba, podniesiona do kwadratu, daje wynik dodatni. W związku z tym cała delta zapisana jako \(b^2+60\) jest na pewno dodatnia. Dodatnia delta oznacza, że mamy dwa miejsca zerowe. Tak więc ta funkcja ma dwa miejsca zerowe, ponieważ \(b^2+60\gt0\).
- Odpowiedź:
A., ponieważ 1.
Przykładowe zadanie:
Dana jest funkcja \(y=f(x)\), której wykres przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku obok.
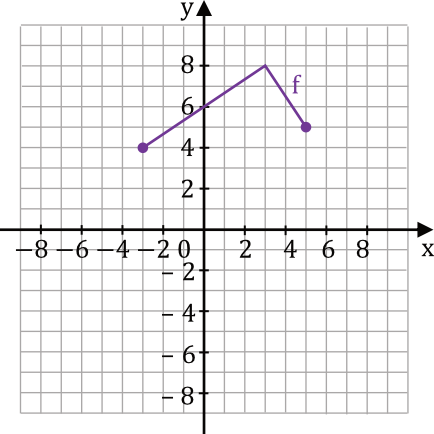
Ta funkcja jest określona dla \(x\in\langle−3, 5\rangle\). Funkcje \(g\) oraz \(h\) są określone za pomocą funkcji \(f\) następująco:
$$y=g(x)=f(x+2) \quad\quad\quad y=h(x)=f(-x)$$
Na rysunkach A-F przedstawiono wykresy różnych funkcji – w tym wykresy funkcji \(g\) oraz \(h\). Każdej z funkcji \(y=g(x)\) oraz \(y=h(x)\) przyporządkuj jej wykres. Wpisz obok symboli funkcji w tabeli poniżej właściwe odpowiedzi wybrane spośród A-F.
| Zadanie | Funkcja | Rysunek |
| 1. | \(y=g(x)\) | |
| 2. | \(y=h(x)\) |
- Rozwiązanie:
Zapis \(g(x)=f(x+2)\) oznacza, że funkcja \(g(x)\) jest wynikiem przesunięcia funkcji \(f(x)\) o dwie jednostki w lewo. Taką sytuację mamy na rysunku D.Zapis \(h(x)=f(-x)\) oznacza, że funkcja \(h(x)\) jest wynikiem przekształcenia funkcji \(f(x)\) względem osi \(OY\) (czyli takim odbiciem lustrzanym względem osi \(OX\)). Taką sytuację mamy na rysunku B.
- Odpowiedź:
1. D oraz 2. B
Wśród zadań otwartych znajdą się m.in.:
Przykładowe zadanie:
Dana jest funkcja \(y=f(x)\), której wykres przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku obok. Ta funkcja jest określona dla każdej liczby rzeczywistej \(x\in\langle-5,8\rangle\).
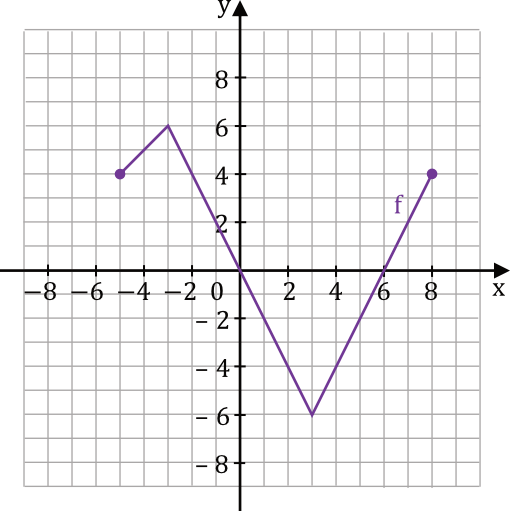
Największa wartość funkcji \(f\) jest równa liczbie \(……………\) , a najmniejsza wartość funkcji \(f\) jest równa liczbie \(……………\) .
- Rozwiązanie:
Spoglądamy na naszą funkcję i sprawdzamy, jakie są największe i najmniejsze wartości przez nią przyjmowane. Widzimy, że największą przyjmowaną wartością jest \(y=6\), natomiast najmniejszą będzie \(y=-6\). - Odpowiedź:
\(y=6\) oraz \(y=-6\)
Przykładowe zadanie:
Rozwiąż równanie:
$$\frac{(4x+1)(x-5)}{(2x-10)(x+3)}=0$$
- Rozwiązanie:
Krok 1. Zapisanie założeń.
Mamy równanie, w którym niewiadoma \(x\) pojawia się w mianowniku ułamka. Zanim więc zaczniemy cokolwiek obliczać, musimy zapisać stosowne założenia, ponieważ wartość mianownika nie może być równa \(0\) (gdyż na matematyce nie istnieje dzielenie przez \(0\)). Skoro tak, to:
$$(2x-10)(x+3)\neq0$$Mamy postać iloczynową równania kwadratowego, zatem każdy z nawiasów musi być różny od zera, czyli:
$$2x-10\neq0 \quad\land\quad x+3\neq0 \\
2x\neq10 \quad\land\quad x\neq-3 \\
x\neq5 \quad\land\quad x\neq-3$$Krok 2. Rozwiązanie równania.
Aby rozwiązać podane równanie, musimy obydwie strony pomnożyć przez wartość w mianowniku, zatem:
$$\frac{(4x+1)(x-5)}{(2x-10)(x+3)}=0 \quad\bigg/\cdot(2x-10)(x+3) \\
(4x+1)(x-5)=0$$Otrzymaliśmy równanie kwadratowe w postaci iloczynowej, zatem przyrównujemy wartości w nawiasach do zera:
$$4x+1=0 \quad\lor\quad x-5=0 \\
4x=-1 \quad\lor\quad x=5 \\
x=-\frac{1}{4} \quad\lor\quad x=5$$Krok 3. Weryfikacja otrzymanych wyników.
Na koniec musimy zweryfikować otrzymane wyniki z zapisanymi założeniami. Widzimy, że rozwiązanie \(x=5\) musimy odrzucić, bo dla tej wartości mianownik był równy \(0\). Skoro tak, to jedynym rozwiązaniem tego zadania będzie \(x=-\frac{1}{4}\). - Odpowiedź:
\(x=-\frac{1}{4}\)
Przykładowe zadanie:
Wierzchołki \(A\) i \(C\) trójkąta \(ABC\) leżą na okręgu o promieniu \(r\). Środek \(S\) tego okręgu leży na boku \(AB\) tego trójkąta (zobacz rysunek poniżej). Długości boków \(AB\) i \(AC\) są równe odpowiednio \(|AB|=3r\) oraz \(|AC|=\sqrt{3}r\).
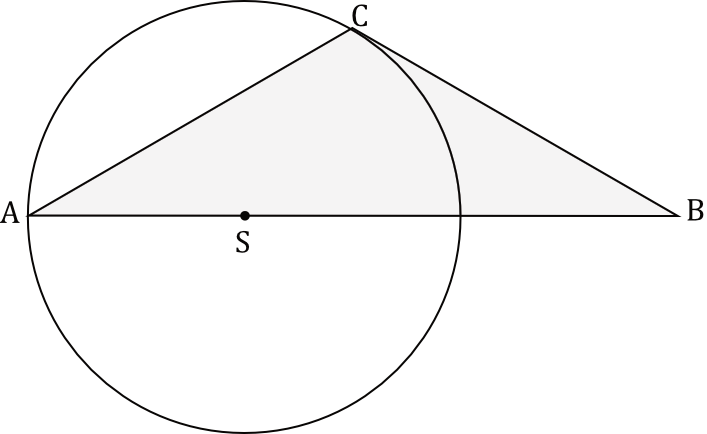
Oblicz miary wszystkich kątów trójkąta \(ABC\).
- Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego.
Zwróćmy uwagę, że z wierzchołka \(C\) możemy dorysować bok w taki sposób, że otrzymamy trójkąt oparty na średnicy okręgu. Z własności trójkątów wiemy, że taki trójkąt oparty na średnicy będzie zawsze prostokątny i to będzie punkt wyjścia do dalszych obliczeń. Nanosząc dane z treści zadania otrzymamy następujący rysunek szkicowy:
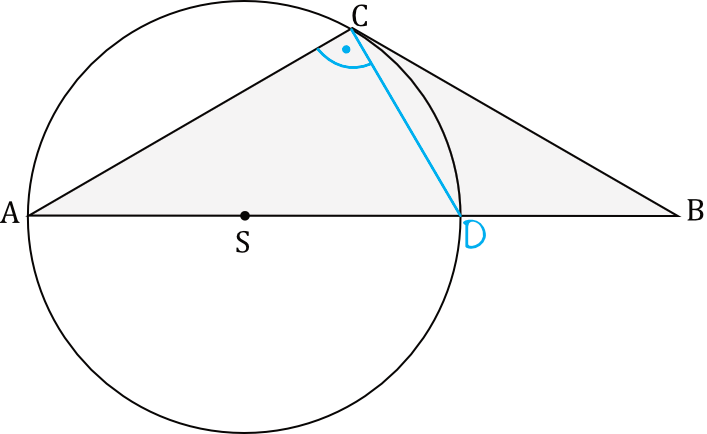
Ustalmy jeszcze skąd wiemy, że odcinek \(DB\) ma długość \(r\). Z treści zadania wynika, że \(|AB|=3r\), a skoro odcinek \(AS\) ma długość \(r\) oraz \(SD\) ma długość \(r\), to odcinek \(DB\) musi mieć \(3r-2r=r\).
Krok 2. Obliczenie długości odcinka \(CD\).
Skoro trójkąt \(ACD\) jest prostokątny, to możemy skorzystać z Twierdzenia Pitagorasa.$$|AC|^2+|CD|^2=|AD|^2 \\
(\sqrt{3}r)^2+|CD|^2=(2r)^2 \\
3r^2+|CD|^2=4r^2 \\
|CD|^2=r^2 \\
|CD|=r \quad\lor\quad |CD|=-r$$Ujemną długość oczywiście odrzucamy, zatem \(|CD|=r\).
Krok 3. Dostrzeżenie trójkąta o kątach \(30°, 60°, 90°\).
Powinniśmy zauważyć, że trójkąt \(ADC\) jest trójkątem o kątach \(30°, 60°, 90°\). Wynika to wprost z własności trójkąta, gdyż jedna przyprostokątna ma długość \(r\), a przeciwprostokątna ma \(2r\), czyli jest dwa razy od niej dłuższa. Dodatkowo druga przyprostokątna jest \(\sqrt{3}\) razy większa od pierwszej. To wszystko to cechy charakterystyczne właśnie dla trójkątów o kątach \(30°, 60°, 90°\).W związku z tym \(|\sphericalangle CAD|=30°\) oraz \(|\sphericalangle ADC|=60°\).
Krok 4. Obliczenie miary kąta \(CDB\).
Spójrzmy na kąt \(CBD\). Jest to kąt przyległy do kąta o mierze \(60°\), a wiemy, że suma miar kątów przyległych jest zawsze równa \(180°\). Skoro tak, to:
$$|\sphericalangle CDB|=180°-60°=120°$$Krok 5. Obliczenie pozostałych miar kątów trójkąta \(DBC\) oraz \(ABC\).
Wiemy już, że trójkąt \(DBC\) jest trójkątem równoramiennym (ramiona o długości \(r\)). Kąt między tymi ramionami ma miarę \(120°\), a więc na dwa pozostałe kąty zostało nam \(180°-120°=60°\). Kąty przy podstawie \(BC\) będą jednakowej miary (wynika to wprost z własności trójkątów równoramiennych), zatem każdy z nich będzie miał \(60°:2=30°\). Mamy więc następującą sytuację:
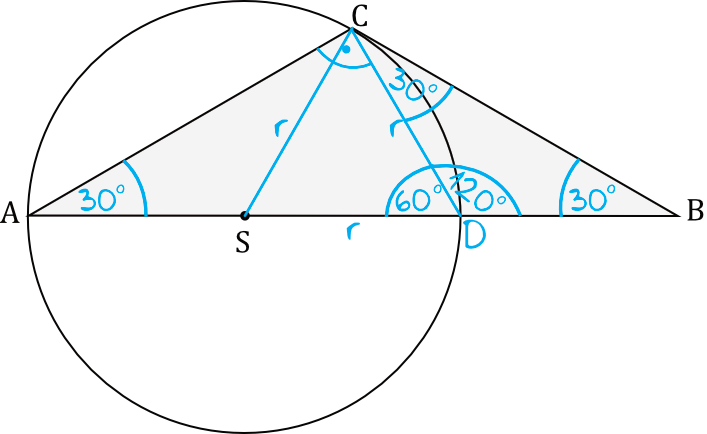
Zadanie polega na podaniu miar kątów trójkąta \(ABC\), a więc:
$$|\sphericalangle CAB|=30° \\
|\sphericalangle ABC|=30° \\
|\sphericalangle BCA|=90°+30°=120°$$ - Odpowiedź:
\(30°, 30°, 120°\)
Przykładowe zadanie:
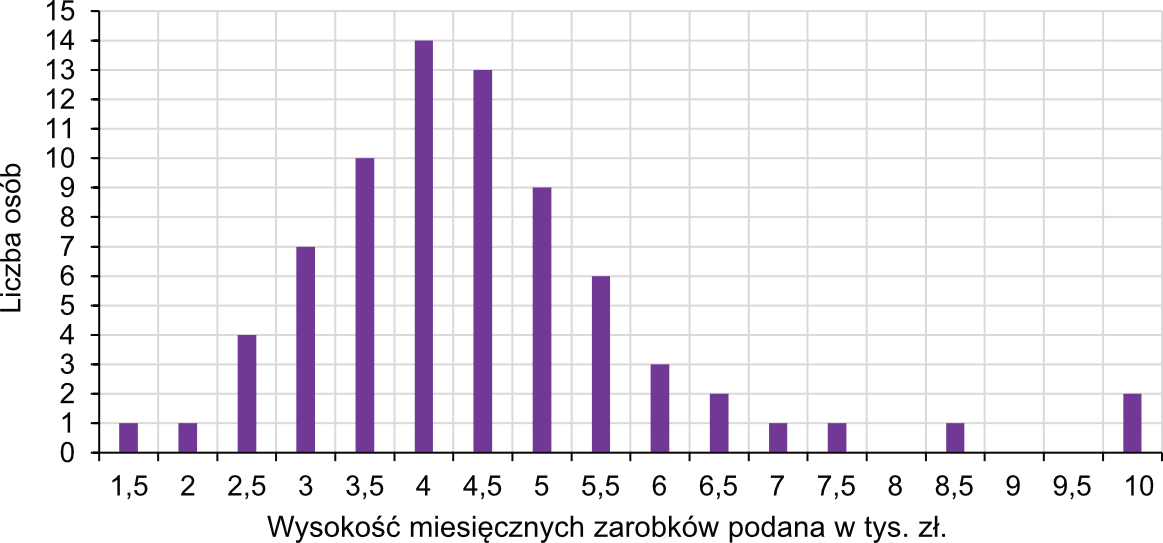
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie \(F\). Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy \(F\), a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
Zadanie 1.
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Dominantą miesięcznych zarobków w firmie \(F\) jest:
| A. \(10\) tys. zł | ponieważ | 1. tę wartość zarobków osiąga najwięcej osób w firmie \(F\). |
| B. \(4,5\) tys. zł | 2. ta wartość zarobków jest największa w firmie \(F\). | |
| C. \(4\) tys. zł | 3. iloczyn tej wartości zarobków i liczby osób z takimi zarobkami jest największy w firmie \(F\). |
Zadanie 2.
Uzupełnij zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu, aby zdanie było prawdziwe.
Medianą miesięcznych zarobków w firmie \(F\) jest \(……………..\) tys. zł.
Zadanie 3.
Oblicz, jaki \(\%\) liczby wszystkich pracowników firmy \(F\) stanowią osoby zarabiające \(5,5\) tys. zł lub mniej.
Zadanie 4.
Oblicz średnią miesięcznego wynagrodzenia netto wszystkich pracowników firmy \(F\). Wynik podaj bez zaokrąglania.
- Rozwiązanie:
Rozwiązanie zadania 1.
Dominanta to wartość, która występuje najczęściej. Z wykresu możemy odczytać, że najwięcej osób zarabia \(4\) tysiące złotych. To oznacza, że dominanta miesięcznych zarobków wynosi \(4\) tys. zł ponieważ tę wartość zarobków osiąga najwięcej osób w firmie \(F\).Rozwiązanie zadania 2.
Krok 1. Obliczenie liczby pracowników.
Aby poznać liczbę pracowników tej firmy, musimy zsumować liczbę osób pobierających dane wynagrodzenie (np. \(1\) osoba zarabia \(1,5\) tysiąca, \(1\) osoba zarabia \(2\) tysiące, \(4\) osoby zarabiają \(2,5\) tysiąca itd.). To oznacza, że tych pracowników będziemy mieć:
$$1+1+4+7+10+14+13+9+6+3+2+1+1+1+2=75$$Krok 2. Obliczenie mediany.
Mamy nieparzystą liczbę pracowników, a to oznacza, że mediana będzie równa tak zwanej środkowej wartości. W przypadku ciągu \(75\)-elementowego, środkową wartością będzie pensja numer \(38\).Teoretycznie powinniśmy teraz wypisać wszystkie zarobki w ciągu niemalejącym (od najmniejszej do największej wypłaty) i wybrać tę, która będzie trzydziesta ósma w kolejności. Oczywiście nie będziemy zapisywać po kolei tych wszystkich pensji – wystarczy zauważyć, że \(1+1+4+7+10+14=37\) osób zarabia \(4\) tysiące lub mniej. Nas interesują zarobki \(38.\) osoby, a te wynoszą w takim razie \(4,5\) tysiąca złotych. Stąd też mediana zarobków wynosi właśnie \(4,5\) tysiąca złotych.
Rozwiązanie zadania 3.
Osób zarabiających \(5,5\) tysiąca złotych lub mniej mamy:
$$1+1+4+7+10+14+13+9+6=65$$Wszystkich pracowników mamy \(75\), więc ci zarabiający \(5,5\) tys. zł lub mniej stanowią:
$$\frac{65}{75}\cdot100\%=86\frac{2}{3}\%$$Rozwiązanie zadania 4.
Aby obliczyć średnią, musimy zsumować wszystkie wynagrodzenia i podzielić to przez liczbę wszystkich pracowników. Suma wszystkich wynagrodzeń będzie równa:
$$1\cdot1,5+1\cdot2+4\cdot2,5+7\cdot3+10\cdot3,5+14\cdot4+13\cdot4,5+ \\
+9\cdot5+6\cdot5,5+3\cdot6+2\cdot6,5+1\cdot7+1\cdot7,5+1\cdot8,5+2\cdot10= \\
=1,5+2+10+21+35+56+58,5+45+33+18+13+7+7,5+8,5+20=336$$Wiemy już, że mamy \(75\) pracowników, zatem średnia będzie równa:
$$śr=\frac{336}{75} \\
śr=4,48$$Średnia pensja wynosi więc \(4480zł\).
- Odpowiedź:
1. C., ponieważ 1.
2. \(4,5\)
3. \(86\frac{2}{3}\%\)
4. \(4480zł\)
Do tej pory na maturach pojawiało się wszystko to, co znajdowało się w podręcznikach i czego uczyliśmy się w szkole. Na maturze 2023 i 2024 zakres podstawy egzaminacyjnej nie będzie pokrywać się z podstawą programową (będzie on okrojony). Przykładowo: na pewno omawiałeś/aś w szkole bryły obrotowe, a tych na maturze 2023 i 2024 mieć nie będziemy. Abyście nie musieli przekopywać się przez informatory i aneksy, pokażę kluczowe zmiany między starą i nową maturą.
Tematy, które doszły (względem starej matury):
– działania na wielomianach;
– równania i nierówności z wartością bezwzględną;
– nowe typy równań trzeciego i wyższego stopnia (metoda wyłączania wspólnego czynnika przed nawias oraz metoda grupowania);
– twierdzenie cosinusów (ale bez twierdzenia sinusów);
– równanie okręgu;
– dominanta.
Tematy, które odpadły (względem starej matury):
– błąd bezwzględny i względny;
– bryły obrotowe.
Można więc powiedzieć, że zakres zagadnień egzaminacyjnych jest szerszy niż był do tej pory, ale jednocześnie jest mniejszy niż to, co będzie od 2025 roku. Przykładowo, uczniowie od 2025 roku będą mieli dodatkowo m.in.:
– wzory skróconego mnożenia trzeciego stopnia;
– układy równań z równaniem kwadratowym;
– równania dwukwadratowe;
– ciągi rekurencyjne;
– twierdzenie sinusów;
– bryły obrotowe.
Jeśli chcesz wiedzieć jak wygląda cała nowa podstawa egzaminacyjna na rok 2023 i 2024, to prezentuje się ona następująco:
Zdający:
1) wykonuje działania (dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie, pierwiastkowanie, logarytmowanie) w zbiorze liczb rzeczywistych;
2) przeprowadza proste dowody dotyczące podzielności liczb całkowitych i reszt z dzielenia nie trudniejsze niż dowód podzielności przez 24 iloczynu czterech kolejnych liczb naturalnych;
3) stosuje własności pierwiastków dowolnego stopnia, w tym pierwiastków stopnia nieparzystego z liczb ujemnych;
4) stosuje związek pierwiastkowania z potęgowaniem oraz prawa działań na potęgach i pierwiastkach;
5) stosuje własności monotoniczności potęgowania, w szczególności własności: jeśli \(x\lt y\) oraz \(a\gt 1\), to \(a^x \lt a^y\), zaś gdy \(x\lt y\) i \(0\lt a\lt1\), to \(a^x\gt a^y\);
6) posługuje się pojęciem przedziału liczbowego, zaznacza przedziały na osi liczbowej;
7) stosuje interpretację geometryczną i algebraiczną wartości bezwzględnej, rozwiązuje równania i nierówności typu: \(|x+4|=5\), \(|x-2|\lt3\), \(|x+3|\ge4\);
8) wykorzystuje własności potęgowania i pierwiastkowania w sytuacjach praktycznych, w tym do obliczania procentów składanych z kapitalizacją roczną i zysków z lokat;
9) stosuje związek logarytmowania z potęgowaniem, posługuje się wzorami na logarytm iloczynu, logarytm ilorazu i logarytm potęgi.
Zdający:
1) stosuje wzory skróconego mnożenia na: \((a+b)^2\), \((a-b)^2\), \(a^2-b^2\);
2) dodaje, odejmuje i mnoży wielomiany jednej i wielu zmiennych;
3) wyłącza poza nawias jednomian z sumy algebraicznej;
4) rozkłada wielomiany na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów, w przypadkach nie trudniejszych niż rozkład wielomianu \(W(x)=2x^3-\sqrt{3}x^2+4x-2\sqrt{3}\);
5) mnoży i dzieli wyrażenia wymierne;
6) dodaje i odejmuje wyrażenia wymierne, w przypadkach nie trudniejszych niż:
\(\frac{1}{x+1}-\frac{1}{x}\), \(\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x^3}\), \(\frac{x+1}{x+2}+\frac{x-1}{x+1}\).
Zdający:
1) przekształca równania i nierówności w sposób równoważny;
2) interpretuje równania i nierówności sprzeczne oraz tożsamościowe;
3) rozwiązuje nierówności liniowe z jedną niewiadomą;
4) rozwiązuje równania i nierówności kwadratowe;
5) rozwiązuje równania wielomianowe postaci \(W(x)=0\) dla wielomianów doprowadzonych do postaci iloczynowej lub takich, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania;
6) rozwiązuje równania wymierne postaci \(\frac{V(x)}{W(x)}=0\), gdzie wielomiany \(V(x)\) i \(W(x)\) są zapisane w postaci iloczynowej.
Zdający:
1) rozwiązuje układy równań liniowych z dwiema niewiadomymi, podaje interpretację geometryczną układów oznaczonych, nieoznaczonych i sprzecznych;
2) stosuje układy równań do rozwiązywania zadań tekstowych.
Zdający:
1) określa funkcje jako jednoznaczne przyporządkowanie za pomocą opisu słownego, tabeli, wykresu, wzoru (także różnymi wzorami na różnych przedziałach);
2) oblicza wartość funkcji zadanej wzorem algebraicznym;
3) odczytuje i interpretuje wartości funkcji określonych za pomocą tabel, wykresów, wzorów itp., również w sytuacjach wielokrotnego użycia tego samego źródła informacji lub kilku źródeł jednocześnie;
4) odczytuje z wykresu funkcji: dziedzinę, zbiór wartości, miejsca zerowe, przedziały monotoniczności, przedziały, w których funkcja przyjmuje wartości większe (nie mniejsze) lub mniejsze (nie większe) od danej liczby, największe i najmniejsze wartości funkcji (o ile istnieją) w danym przedziale domkniętym oraz argumenty, dla których wartości największe i najmniejsze są przez funkcję przyjmowane;
5) interpretuje współczynniki występujące we wzorze funkcji liniowej;
6) wyznacza wzór funkcji liniowej na podstawie informacji o jej wykresie lub o jej własnościach;
7) szkicuje wykres funkcji kwadratowej zadanej wzorem;
8) interpretuje współczynniki występujące we wzorze funkcji kwadratowej w postaci ogólnej, kanonicznej i iloczynowej (jeśli istnieje);
9) wyznacza wzór funkcji kwadratowej na podstawie informacji o tej funkcji lub o jej wykresie;
10) wyznacza największą i najmniejszą wartość funkcji kwadratowej w przedziale domkniętym;
11) wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp., także osadzonych w kontekście praktycznym;
12) na podstawie wykresu funkcji \(y=f(x)\) szkicuje wykresy funkcji \(y=f(x-a)\), \(y=f(x)+b\), \(y=-f(x)\), \(y=f(-x)\);
13) posługuje się funkcjami wykładniczą i logarytmiczną, w tym ich wykresami, do opisu i interpretacji zagadnień związanych z zastosowaniami praktycznymi.
Zdający:
1) oblicza wyrazy ciągu określonego wzorem ogólnym;
2) w prostych przypadkach bada, czy ciąg jest rosnący, czy malejący;
3) sprawdza, czy dany ciąg jest arytmetyczny lub geometryczny;
4) stosuje wzór na \(n\)-ty wyraz i na sumę \(n\) początkowych wyrazów ciągu arytmetycznego;
5) stosuje wzór na \(n\)-ty wyraz i na sumę \(n\) początkowych wyrazów ciągu geometrycznego;
6) wykorzystuje własności ciągów, w tym arytmetycznych i geometrycznych, do rozwiązywania zadań, również osadzonych w kontekście praktycznym.
Zdający:
1) wykorzystuje definicje funkcji: sinus, cosinus i tangens dla kątów od \(0°\) do \(180°\), w szczególności wyznacza wartości funkcji trygonometrycznych dla
kątów \(30°, 45°, 60°\);
2) korzysta z wzorów \(sin^2\alpha+cos^2\alpha=1, tg\alpha=\frac{sin\alpha}{cos\alpha}\);
3) stosuje twierdzenie cosinusów oraz wzór na pole trójkąta \(P=\frac{1}{2}\cdot a\cdot b\cdot sin\gamma\);
4) oblicza kąty trójkąta i długości jego boków przy odpowiednich danych (rozwiązuje trójkąty m.in. z wykorzystaniem twierdzenia cosinusów).
Zdający:
1) wyznacza promienie i średnice okręgów, długości cięciw okręgów oraz odcinków stycznych, w tym z wykorzystaniem twierdzenia Pitagorasa;
2) rozpoznaje trójkąty ostrokątne, prostokątne i rozwartokątne przy danych długościach boków (m.in. stosuje twierdzenie odwrotne do twierdzenia Pitagorasa i twierdzenie cosinusów); stosuje twierdzenie: w trójkącie naprzeciw większego kąta wewnętrznego leży dłuższy bok;
3) rozpoznaje wielokąty foremne i korzysta z ich podstawowych własności;
4) korzysta z własności kątów i przekątnych w prostokątach, równoległobokach, rombach i trapezach;
5) stosuje własności kątów wpisanych i środkowych;
6) stosuje wzory na pole wycinka koła i długość łuku okręgu;
7) stosuje twierdzenia: Talesa, o dwusiecznej kąta oraz o kącie między styczną a cięciwą;
8) korzysta z cech podobieństwa trójkątów;
9) wykorzystuje zależności między obwodami oraz między polami figur podobnych;
10) wskazuje podstawowe punkty szczególne w trójkącie: środek okręgu wpisanego w trójkąt, środek okręgu opisanego na trójkącie, środek ciężkości oraz korzysta z ich własności;
11) stosuje funkcje trygonometryczne do wyznaczania długości odcinków w figurach płaskich oraz obliczania pól figur.
Zdający:
1) rozpoznaje wzajemne położenie prostych na płaszczyźnie na podstawie ich równań, w tym znajduje wspólny punkt dwóch prostych, jeśli taki istnieje;
2) posługuje się równaniem prostej na płaszczyźnie w postaci kierunkowej, w tym wyznacza równanie prostej o zadanych własnościach (takich jak na przykład przechodzenie przez dwa dane punkty, znany współczynnik kierunkowy, równoległość lub prostopadłość do innej prostej, styczność do okręgu);
3) oblicza odległość dwóch punktów w układzie współrzędnych;
4) posługuje się równaniem okręgu \((x-a)^2+(y-b)^2=r^2\);
5) oblicza odległość punktu od prostej;
6) wyznacza obrazy okręgów i wielokątów w symetriach osiowych względem osi układu współrzędnych, symetrii środkowej (o środku w początku układu współrzędnych).
Zdający:
1) rozpoznaje wzajemne położenie prostych w przestrzeni, w szczególności proste prostopadłe nieprzecinające się;
2) posługuje się pojęciem kąta między prostą a płaszczyzną;
3) rozpoznaje w graniastosłupach i ostrosłupach kąty między odcinkami (np. krawędziami, krawędziami i przekątnymi), oblicza miary tych kątów;
4) oblicza objętości i pola powierzchni graniastosłupów i ostrosłupów, również z wykorzystaniem trygonometrii i poznanych twierdzeń;
5) wykorzystuje zależność między objętościami graniastosłupów oraz ostrosłupów podobnych.
Zdający:
1) zlicza obiekty w prostych sytuacjach kombinatorycznych;
2) zlicza obiekty, stosując reguły mnożenia i dodawania (także łącznie) dla dowolnej liczby czynności w sytuacjach nie trudniejszych niż:
a) obliczenie, ile jest czterocyfrowych nieparzystych liczb całkowitych dodatnich takich, że w ich zapisie dziesiętnym występuje dokładnie jedna cyfra \(1\) i dokładnie jedna cyfra \(2\),
b) obliczenie, ile jest czterocyfrowych parzystych liczb całkowitych dodatnich takich, że w ich zapisie dziesiętnym występuje dokładnie jedna cyfra \(0\) i dokładnie jedna cyfra \(1\).
Zdający:
1) oblicza prawdopodobieństwo w modelu klasycznym;
2) oblicza średnią arytmetyczną i średnią ważoną, znajduje medianę i dominantę;
3) oblicza odchylenie standardowe zestawu danych (także w przypadku danych odpowiednio pogrupowanych), interpretuje ten parametr dla danych empirycznych.
Zdający rozwiązuje zadania optymalizacyjne w sytuacjach dających się opisać funkcją kwadratową.
Mam dla Was świetną wiadomość! Matbryk (czyli moje autorskie repetytorium maturalne) jest już przystosowany do matury 2023 i 2024. To jedna z nielicznych książek na rynku, która jest dopasowana do nowych wymagań egzaminacyjnych, dlatego tym bardziej zachęcam Was do jej zakupu. W tym miejscu ślę szczególne podziękowania dla uczniów z poprzednich roczników, którzy tak chętnie korzystali z Matbryka, bo to właśnie dzięki nim książka cieszy się sporą popularnością, co pozwala mi robić kolejne dodruki i nowe edycje.
A jeśli dotarłeś/aś już do tego miejsca, to mam dla Ciebie małą promocję, oto szczegóły:


Matbryka możesz kupić też w promocyjnym pakiecie z dostępem video do Szalonych Liczb! Pakiet pozwala zaoszczędzić 50% na dostępie premium oraz gwarantuje darmową dostawę :)




Witam, pisałam maturę w 2020, ale jej nie zdałam, w 2023 planuje podejść znów na jakich zasadach będę zdawać tą maturę? Nie wiem, od czego zacząć bo jestem trochę nie w temacie.
Powiem szczerze, że niestety nie znam odpowiedzi na to pytanie :( Wydaje mi się, że najlepiej byłoby się odezwać wprost do CKE, bo nie chciałbym Cię wprowadzić w błąd. Swoją drogą jak ktoś z czytających będzie wiedział jak to wygląda w praktyce, to będę wdzięczny za komentarz ;)
Witam, zanim zainwestuję chciałabym się dowiedzieć czy zbiór zawiera zadania podzielone tematycznie czy w formie egzaminu i jak dużo jest tych zadań. Pozdrawiam Katarzyna
Chodzi o Matbryka? :) Jeśli tak, to tam zadania są podzielone tematycznie – jest to ponad 40 rozdziałów i około 450 zadań z pełnymi rozwiązaniami :)
Czy Matbryk zawiera nowe typy zadań?
Zawiera! Jedną ze zmian w nowym wydaniu jest właśnie to, że część zadań ze starej wersji przerobiłem na te nowe typy (np. prawda/fałsz), no i do tego doszło też sporo nowych zadań :)
Czyli bryły obrotowe i ostrosłupy odpadają także w formule 2015?
Bryły obrotowe odpadają :) Co do ostrosłupów – odpadają duże/rozbudowane zadania z ostrosłupami, gdzie np. wykorzystamy trygonometrię, ale mogą się pojawić proste zadania związane chociażby z obliczeniem objętości graniastosłupa/ostrosłupa :)
Czy matura 2024, będzie miała okrojoną ilość zadań tak jak do tej pory dla nowej2023 jak i starej formuły 2015 (jeśli ktoś poprawia w 2024 a pisał starą formułę 2015)
Matura 2023 będzie dokładnie taka sama jak 2024 :) Więcej zadań i więcej materiału będzie dopiero od matury 2025 :)
Czy na maturze 2024 będą zadania – Błędów bezwzględnych/względnych?
Na 100% nie będzie :)