Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Wykres funkcji \(f(x)=2^x+3\) jest tak naprawdę przesunięciem wykresu funkcji wykładniczej \(2^x\) o trzy jednostki w górę. Jeżeli nie pamiętamy jak rysuje się funkcje wykładnicze, to zawsze możemy podstawić sobie do wzoru kilka iksów i sprawdzić jaką wartość przyjmie funkcja dla tych konkretnych argumentów. Przykładowo:
Dla \(x=0\) funkcja \(f(x)=2^x\) przyjmuje wartość \(y=2^0=1\)
Dla \(x=1\) funkcja \(y=2^x\) przyjmuje wartość \(y=2^1=2\)
Dla \(x=2\) funkcja \(y=2^x\) przyjmuje wartość \(y=2^2=4\)
Dla \(x=-1\) funkcja \(y=2^x\) przyjmuje wartość \(y=2^{-1}=\frac{1}{2}\)
Funkcja \(f(x)=2^x+3\) będzie przyjmować zawsze wartości o \(3\) większe od funkcji \(f(x)=2^x\). Spróbujmy zatem narysować ten wykres:
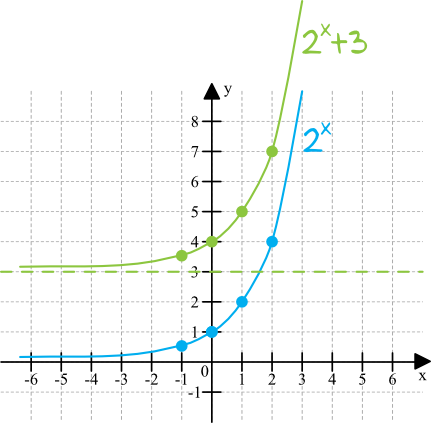
Krok 2. Odczytanie zbioru wartości funkcji.
Szukamy zbioru wartości, czyli patrzymy na oś igreków. Widzimy wyraźnie, że funkcja przyjmuje wartości większe od \(3\) i idzie aż do nieskończoności, zatem zbiorem wartości funkcji jest \((3,+\infty)\).