Wyznacz równanie okręgu przechodzącego przez punkt \(A=(2,1)\) i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
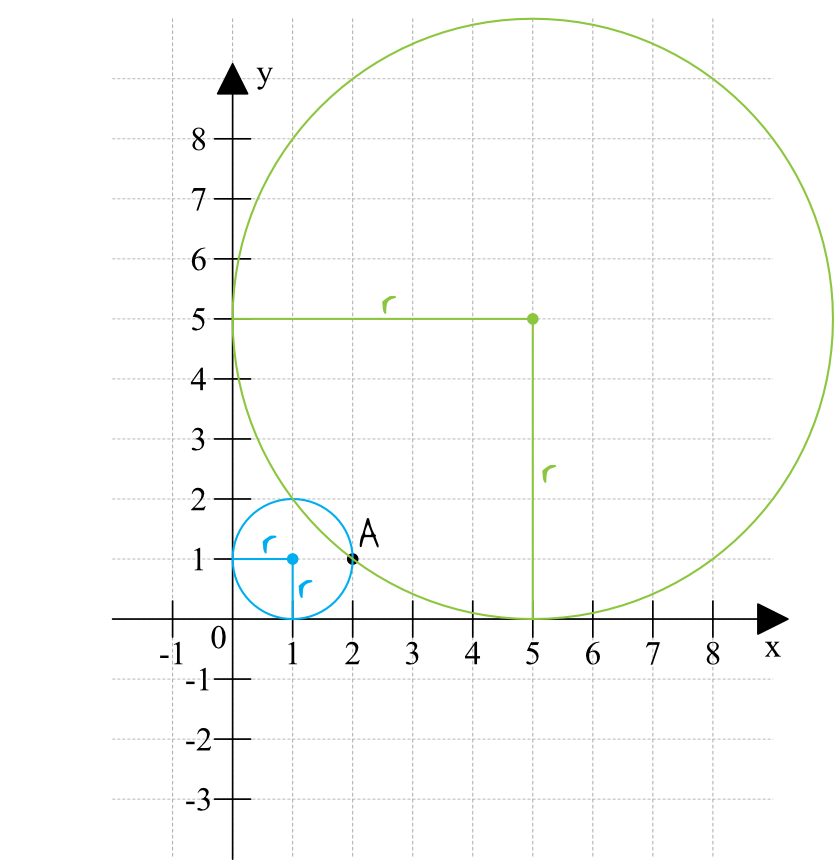
Wnioski jakie płyną z tego rysunku są następujące:
– na pewno ten okrąg (a w zasadzie okręgi) będą leżeć w pierwszej ćwiartce układu współrzędnych, bo nie ma innej możliwości skoro muszą przechodzić przez punkt \(A=(2;1)\).
– w każdym przypadku odległość od obu osi jest równa promieniowi okręgu. Skoro tak, to środek każdego z okręgów będzie przybierał postać typu \(S=(r;r)\).
Wiemy z tablic matematycznych, że wzór na równanie okręgu ma postać:
$$(x-r)^2+(y-r)^2=r^2$$
Podstawiając pod ten wzór współrzędne punktu \(A=(2;1)\) przez które okrąg przechodzi (czyli \(x=2\), \(y=1)\) otrzymamy:
$$(2-r)^2+(1-r)^2=r^2 \\
4-4r+r^2+1-2r+r^2=r^2 \\
2r^2-6r+5=r^2 \\
r^2-6r+5=0$$
Współczynniki: \(a=1,\;b=-6,\;c=5\)
$$Δ=b^2-4ac=(-6)^2-4\cdot1\cdot5=36-20=16 \\
\sqrt{Δ}=\sqrt{16}=4$$
$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-6)-4}{2\cdot1}=\frac{6-4}{2}=\frac{2}{2}=1 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-6)+4}{2\cdot1}=\frac{6+4}{2}=\frac{10}{2}=5$$
Otrzymaliśmy dwie możliwości \(r=1 \quad\lor\quad r=5\). Obydwie możliwości są poprawne, żadnej nie odrzucamy (moglibyśmy odrzucić gdyby np. jedna z wartości była ujemna). To oznacza, że otrzymamy dwa równania okręgów:
Okrąg mniejszy: \((x-1)^2+(y-1)^2=1^2\), czyli \((x-1)^2+(y-1)^2=1\)
Okrąg większy: \((x-5)^2+(y-5)^2=5^2\), czyli \((x-5)^2+(y-5)^2=25\)
Istnieją dwa okręgi, które spełniają warunki zadania, dlatego są dwie możliwości równań tychże okręgów: \((x-1)^2+(y-1)^2=1\) oraz \((x-5)^2+(y-5)^2=25\).

