Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
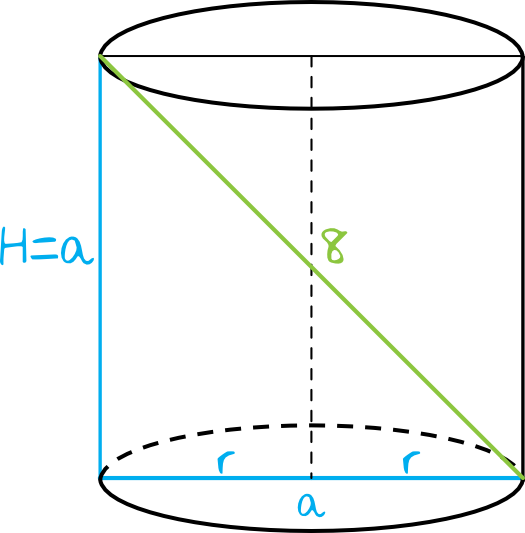
Krok 2. Obliczenie długości krawędzi kwadratu.
Z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). W związku z tym:
$$a\sqrt{2}=8 \\
a=\frac{8}{\sqrt{2}} \\
a=\frac{8\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a=\frac{8\sqrt{2}}{2} \\
a=4\sqrt{2}$$
To oznacza, że w przekroju znalazł się kwadrat o boku \(4\sqrt{2}\). Zgodnie z naszym rysunkiem oznacza to też, że taka właśnie będzie wysokość walca, czyli \(H=4\sqrt{2}\).
Krok 3. Obliczenie długości promienia.
Promień okręgu znajdującego się w podstawie jest równy połowie boku kwadratu, czyli:
$$r=\frac{1}{2}a \\
r=\frac{1}{2}\cdot4\sqrt{2} \\
r=2\sqrt{2}$$
Krok 4. Obliczenie objętości walca.
Wiemy już, że \(r=2\sqrt{2}\), wiemy też że wysokość walca jest równa \(H=4\sqrt{2}\). To oznacza, że objętość walca będzie równa:
$$V=πr^2\cdot H \\
V=π\cdot(2\sqrt{2})^2\cdot4\sqrt{2} \\
V=π\cdot(4\cdot2)\cdot4\sqrt{2} \\
V=8π\cdot4\sqrt{2} \\
V=32π\sqrt{2}$$