Przekrój osiowy walca jest kwadratem o boku \(a\). Jeżeli \(r\) oznacza promień podstawy walca, \(h\) oznacza wysokość walca, to:
\(r+h=a\)
\(h-r=\frac{a}{2}\)
\(r-h=\frac{a}{2}\)
\(r^2+h^2=a^2\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Spróbujmy sobie narysować pożądany walec i zaznaczmy na nim poszczególne długości:
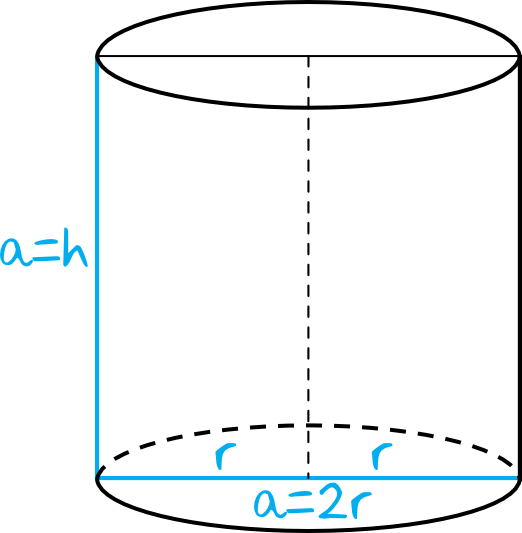
Widzimy wyraźnie, że prawdziwe będą dwie równości:
$$a=2r \\
a=h \\
\text{Zatem }2r=h$$
Krok 2. Wybór prawidłowego równania.
Sprawdźmy teraz po kolei które z równań jest zapisane poprawnie, podstawiając \(a=2r\) oraz \(h=2r\):
Odp. A.
\(r+h=a \\
r+2r=2r \\
3r=2r \\
L\neq P\)
Odp. B.
\(h-r=\frac{a}{2} \\
2r-r=\frac{2r}{2} \\
r=r \\
L=P\)
Odp. C.
\(r-h=\frac{a}{2} \\
r-2r=\frac{2r}{2} \\
-r=r \\
L\neq P\)
Odp. D.
\(r^2+h^2=a^2 \\
r^2+(2r)^2=(2r)^2 \\
r^2+4r^2=4r^2 \\
5r^2=4r^2 \\
L\neq P\)
Prawidłowa zależność znalazła się tylko w drugiej odpowiedzi.
Odpowiedź:
B. \(h-r=\frac{a}{2}\)

